
����Ŀ�����ǿ��Խ�������λ����ʾΪ![]() ������a��b��c �ֱ��ʾ��λ�ϵ����֣�ʮλ�ϵ����ֺ�λ�ϵ����֣���a
������a��b��c �ֱ��ʾ��λ�ϵ����֣�ʮλ�ϵ����ֺ�λ�ϵ����֣���a![]() 0����Ȼ��
0����Ȼ��![]() = 100a+10b+c�����ǰ�����
= 100a+10b+c�����ǰ�����![]() ��
��![]() ��������λ����Ϊһ�����������������x��y��z��������������Ȼ�����磺123��321��һ�����������,789��987��һ�����������.
��������λ����Ϊһ�����������������x��y��z��������������Ȼ�����磺123��321��һ�����������,789��987��һ�����������.
��1��һ������������ĺ�Ϊ1110����������������.
��2�������x��ʾ��λ���֣���˵��������һ������������ĺ��ܱ�37����.
���𰸡���1��456��654����2������һ�ԡ���������ĺ��ܱ�37����.
��������
��1���������������������ֱ��д���������������������������������������һ����λ������ʾ�������������������ͣ���1110����������⣬����жϼ��ɣ�
��2����ʾ����������������������ͣ�д��37��6��x-1�����ж�6��x-1�����������ɣ�
��1��������һ������������е�һ����λ����ʮλ����Ϊx����λ����Ϊ(x![]() 1)��λ����Ϊ(x+1) ��xΪ����1С��9����������
1)��λ����Ϊ(x+1) ��xΪ����1С��9����������
��100��x+1��+10x+x-1=111x+99 ��
�����������100(x-1)+10x+1=111x-99��
������111x+99��+��111x-99��=1110��
��֮�ã�x=5
![]() ��������������456��654��
��������������456��654��
��2��������֪�������λ����λ����Ϊx(xΪ����2С��9������),ʮλ����Ϊx-1,��λ����Ϊx-2��
����������100x+10(x-1)+(x-2)=111x-12��
�������������100(x-2)+10(x-1)+x=111x-210��
������111x-12��+��111x-210��=222x-222=222(x-1) =37![]() 6(x-1)��
6(x-1)��
��Ϊ(x-1)Ϊ������
![]() 37
37![]() 6(x-1)�ܱ�37����.
6(x-1)�ܱ�37����.
![]() ����һ������������ĺ��ܱ�37����.
����һ������������ĺ��ܱ�37����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
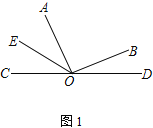
����Ŀ����֪O��ֱ���ϵ�һ�㣬��AOB��ֱ�ǣ�OEƽ�֡�AOC
(1) ��ͼ���У�����BOD��28�������AOE�Ķ���
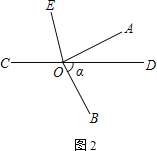
(2) ��ͼ���еġ�AOB�ƶ���O˳ʱ����ת��ͼ�ڵ�λ��������BOD���������ú�����ʽ�ӱ�ʾ��AOE����˵������
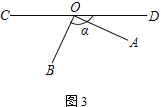
(3) ������תAOB��ͼ�۵�λ�ã�����BOD�����������������䣬�Խ�ͼ�β�������������AOE�Ķ���.���ú�����ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к����У�����y��ֵ��x��ֵ�����������ǣ�������
A.y=��2x
B.y=3x��1
C.y= ![]()
D.y=x2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���̶���һ����1200�ĵ�·�������µ�ʩ����ʽ����Ч������50%�������ǰ4���������
��1����������̶�ԭ�ƻ�ÿ������·�����ף�
��2����������У����Ҫ����ǰ2�����������ôʵ��ƽ��ÿ������·�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ����չ����������������������������������Ŀ������ƹ�����������ë��Ҫ��ÿλѧ��������ֻ��ѡ��һ�Ϊ�˽�ѡ������������Ŀ��ѧ�������������ȡ�˲���ѧ�����е��飬����ͨ�������õ����ݽ������������Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�ش����⣺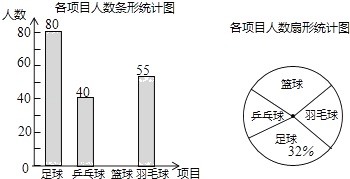
��1����λһ����������ѧ����
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�ѡ��������Ŀ�������������ε�Բ�Ľǵ����ȣ�
��4������ѧУ��1500�ˣ�������Ƹ�ѧУѡ��������Ŀ��ѧ������Լ���ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
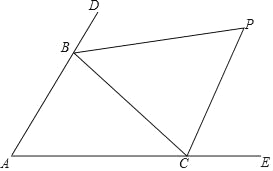
����Ŀ����ͼ����ABC�У��ֱ��ӳ���ABC�ı�AB��AC��D��E����CBD���BCE��ƽ�����ཻ�ڵ�P�������Խ��С����д��ҵ��ʱ�������¹��ɣ�
(1)����A��60�㣬���P���� ���㣻
(2)����A��40�㣬���P���� ���㣻
(3)����A��100�㣬���P���� ���㣻
(4)��������ѧ����ʽ���ɡ�A���P�Ĺ�ϵ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC�У���ACB=90����DΪBC���е㣬DE��AB������ΪE������B��BF��AC��DE���ӳ����ڵ�F������CF��

��1����֤��AD��CF��
��2������AF�����ж���ACF����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B���ֻ����˰��˴��ף�A�ͻ����˱�B�ͻ�����ÿСʱ�����20�����ף�A�ͻ����˰���700��������B�ͻ����˰���500����������ʱ����ȣ���A��B�ͻ�����ÿСʱ�ֱ���˶��ٴ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ھ���ABCD�У�AB��10 cm��BC��8 cm.��P�ӵ�A��������A��B��C��D��·���˶�������Dֹͣ����Q�ӵ�D��������D��C��B��A��·���˶�������Aֹͣ������P����Qͬʱ��������P���ٶ�Ϊÿ��1 cm����Q���ٶ�Ϊÿ��2 cm��a��ʱ����P����Qͬʱ�ı��ٶȣ���P���ٶȱ�Ϊÿ��b cm����Q���ٶȱ�Ϊÿ��d cm.ͼ���ǵ�P����x�����APD�����S1(cm2)��ʱ��x(��)�ĺ�����ϵͼ��ͼ���ǵ�Q����x�����AQD�����S2(cm2)��ʱ��x(��)�ĺ�����ϵͼ����
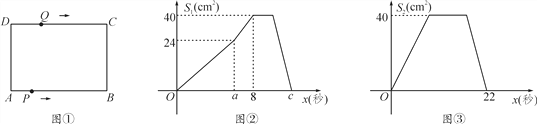
(1)����ͼ�ڣ���a�� b��ͼ����c��ֵ��
(2)��d��ֵ��
(3)���P�뿪��A��·��Ϊy1(cm)����Q����A����Ҫ�ߵ�·��Ϊy2(cm)����ֱ�д���ı��ٶȺ�y1��y2���������˶�ʱ��x(��)�ĺ�����ϵʽ���������P����Q����ʱx��ֵ��
(4)����Q����__ __��ʱ����Q���˶�·��Ϊ25 cm.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com