
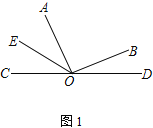
【题目】已知O是直线上的一点,∠AOB是直角,OE平分∠AOC
(1) 在图①中,若∠BOD=28°,求∠AOE的度数
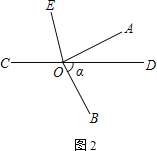
(2) 将图①中的∠AOB绕顶点O顺时针旋转至图②的位置.若∠BOD=α,试用含α的式子表示∠AOE,并说明理由
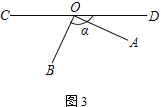
(3) 继续旋转AOB至图③的位置,若∠BOD=α,其他条件不变,试将图形补充完整,求∠AOE的度数.(用含α的式子表示)
【答案】(1)∠AOE=31°;(2)∠AOE=45°+![]() α,理由见解析;(3)作图见解析,∠AOE=135°-
α,理由见解析;(3)作图见解析,∠AOE=135°-![]() α.
α.
【解析】
(1)求出∠AOC,根据角平分线定义求出∠AOE,即可求出答案;
(2)求出∠AOD和∠AOC,根据角平分线定义即可求出答案;
(3)求出∠AOD和∠AOC,根据角平分线定义即可求出答案;
解:(1)∵∠AOB是直角,∠BOD=28°,
∴∠AOC=180°-∠AOB-∠BOD=180°-90°-28°=62°,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×62°=31°;
×62°=31°;
(2)∠AOE=45°+![]() α,理由如下:
α,理由如下:
∵∠AOB是直角,∠BOD=α,
∴∠AOD=90°-α,
∵∠AOD+∠AOC=180°,
∴∠AOC=180°-∠AOD=180°-(90°-α)= 90°+α,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×(90°+α)=45°+
×(90°+α)=45°+![]() α;
α;
(3)如图,
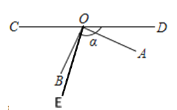
∵∠AOB是直角,∠BOD=α,
∴∠AOD=α-90°,
∵∠AOD+∠AOC=180°,
∴∠AOC=180°-∠AOD=180°-(α-90°)= 270°-α,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×(270°-α)=135°-
×(270°-α)=135°-![]() α.
α.


科目:初中数学 来源: 题型:
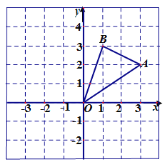
【题目】如图,在边长为1的正方形组成的网格中,三角形AOB的顶点均在格点上,A(3,2),B(1,3),
(1)将三角形AOB先向左平移3个单位长度,后向下平移1个单位得到三角形A1O1B1,请直接作出三角形A1O1B1;
(2)请直接写出三角形A1O1B1三个顶点的坐标;
(3)三角形A1O1B1的面积为_______平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图表示某体校射击队甲、乙两名队员射击比赛的成绩.根据统计图中的信息可得,下列结论正确的是( )

A. 甲队员成绩的平均数比乙队员的大
B. 甲队员成绩的方差比乙队员的大
C. 甲队员成绩的中位数比乙队员的大
D. 乙队员成绩的方差比甲队员的大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

查看答案和解析>>
科目:初中数学 来源: 题型:
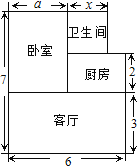
【题目】张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是12000元/m2,面积如图所示(单位:米,卧室的宽为a米,卫生间的宽为x米),
(1) 用含a和x的式子表示该户型的面积
(2) 售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是12 000元/m2,其中厨房只算![]() 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售,
若张先生购买的户型a=3,且分别用两种方案购房金额相等,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
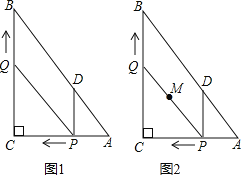
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作
,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作![]() ,交AB于点D,连接PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒
,交AB于点D,连接PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒![]() .
.
![]() 直接用含t的代数式分别表示:
直接用含t的代数式分别表示:![]() ______,
______,![]() ______;
______;
![]() 是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由.
是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由.
![]() 如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A(0,4),B(﹣3,4),C(﹣6,0),动点P从点A出发以1个单位/秒的速度在y轴上向下运动,动点Q同时从点C出发以2个单位/秒的速度在x轴上向右运动,过点P作PD⊥y轴,交OB于D,连接DQ.当点P与点O重合时,两动点均停止运动.设运动的时间为t秒.
(1)当t=1时,求线段DP的长;
(2)连接CD,设△CDQ的面积为S,求S关于t的函数解析式,并求出S的最大值;
(3)运动过程中是否存在某一时刻,使△ODQ与△ABC相似?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们可以将任意三位数表示为![]() (其中a、b、c 分别表示百位上的数字,十位上的数字和个位上的数字,且a
(其中a、b、c 分别表示百位上的数字,十位上的数字和个位上的数字,且a![]() 0)显然,
0)显然,![]() = 100a+10b+c;我们把形如
= 100a+10b+c;我们把形如![]() 和
和![]() 的两个三位数称为一对“姊妹数”(其中x、y、z是三个连续的自然数)如:123和321是一对“姊妹数”,789和987是一对“姊妹数”.
的两个三位数称为一对“姊妹数”(其中x、y、z是三个连续的自然数)如:123和321是一对“姊妹数”,789和987是一对“姊妹数”.
(1)一对“姊妹数”的和为1110,求这对“姊妹数”.
(2)如果用x表示百位数字,试说明:任意一对“姊妹数”的和能被37整除.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com