
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘ŕ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨∂ĮĶ„Pī”Ķ„AŅ™ ľ—ōĪŖACŌÚĶ„C“‘√Ņ√Ž1łŲĶ•őĽ≥§∂»ĶńňŔ∂»‘ň∂Į£¨∂ĮĶ„Qī”Ķ„CŅ™ ľ—ōĪŖCBŌÚĶ„B“‘√Ņ√Ž2łŲĶ•őĽ≥§∂»ĶńňŔ∂»‘ň∂Į£¨ĻżĶ„P◊ų
£¨∂ĮĶ„Pī”Ķ„AŅ™ ľ—ōĪŖACŌÚĶ„C“‘√Ņ√Ž1łŲĶ•őĽ≥§∂»ĶńňŔ∂»‘ň∂Į£¨∂ĮĶ„Qī”Ķ„CŅ™ ľ—ōĪŖCBŌÚĶ„B“‘√Ņ√Ž2łŲĶ•őĽ≥§∂»ĶńňŔ∂»‘ň∂Į£¨ĻżĶ„P◊ų![]() £¨ĹĽAB”ŕĶ„D£¨Ń¨Ĺ”PQ£¨Ķ„P°ĘQ∑÷Īūī”Ķ„A°ĘCÕ¨ Ī≥Ų∑Ę£¨ĶĪ∆š÷–“ĽĶ„ĶĹīÔ∂ňĶ„ Ī£¨ŃŪ“ĽĶ„“≤ňś÷ģÕ£÷Ļ‘ň∂Į£¨…Ť‘ň∂Į Īľšő™t√Ž
£¨ĹĽAB”ŕĶ„D£¨Ń¨Ĺ”PQ£¨Ķ„P°ĘQ∑÷Īūī”Ķ„A°ĘCÕ¨ Ī≥Ų∑Ę£¨ĶĪ∆š÷–“ĽĶ„ĶĹīÔ∂ňĶ„ Ī£¨ŃŪ“ĽĶ„“≤ňś÷ģÕ£÷Ļ‘ň∂Į£¨…Ť‘ň∂Į Īľšő™t√Ž![]() £ģ
£ģ
![]() ÷ĪĹ””√ļ¨tĶńīķ ż Ĺ∑÷ĪūĪŪ ĺ£ļ
÷ĪĹ””√ļ¨tĶńīķ ż Ĺ∑÷ĪūĪŪ ĺ£ļ![]() ______£¨
______£¨![]() ______£Ľ
______£Ľ
![]() «∑Ůīś‘ŕtĶń÷Ķ£¨ ĻňńĪŖ–őPDBQő™∆Ĺ––ňńĪŖ–ő£Ņ»Űīś‘ŕ£¨«ů≥ŲtĶń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£ģ
«∑Ůīś‘ŕtĶń÷Ķ£¨ ĻňńĪŖ–őPDBQő™∆Ĺ––ňńĪŖ–ő£Ņ»Űīś‘ŕ£¨«ů≥ŲtĶń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£ģ
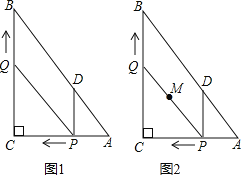
![]() »ÁÕľ2£¨‘ŕ’ŻłŲ‘ň∂ĮĻż≥Ő÷–£¨«ů≥ŲŌŖ∂őPQ÷–Ķ„Mňýĺ≠ĻżĶń¬∑ĺ∂≥§£ģ
»ÁÕľ2£¨‘ŕ’ŻłŲ‘ň∂ĮĻż≥Ő÷–£¨«ů≥ŲŌŖ∂őPQ÷–Ķ„Mňýĺ≠ĻżĶń¬∑ĺ∂≥§£ģ
°ĺīūįł°Ņ£®1£©![]() £¨
£¨![]() £Ľ£®2£©ŌÍľŻĹ‚őŲ£Ľ£®3£©2
£Ľ£®2£©ŌÍľŻĹ‚őŲ£Ľ£®3£©2![]()
°ĺĹ‚őŲ°Ņ
![]() ”…łý囬∑≥ŐĶ»”ŕňŔ∂»≥ň“‘ ĪľšŅ…Ķ√,
”…łý囬∑≥ŐĶ»”ŕňŔ∂»≥ň“‘ ĪľšŅ…Ķ√,![]() ,
,![]() ,‘Ú
,‘Ú![]() ,łýĺ›
,łýĺ›![]() ,
,![]() ,Ņ…Ķ√:
,Ņ…Ķ√:![]() ,łýĺ›Ōŗň∆»żĹ«–őĶńŇ–∂®Ņ…Ķ√:
,łýĺ›Ōŗň∆»żĹ«–őĶńŇ–∂®Ņ…Ķ√:![]() °◊
°◊![]() ,‘Ŕłýĺ›Ōŗň∆»żĹ«–őĶń–‘÷ Ņ…Ķ√:
,‘Ŕłýĺ›Ōŗň∆»żĹ«–őĶń–‘÷ Ņ…Ķ√:
![]() ,ľī
,ľī![]() ,ī”∂ÝĹ‚Ķ√:
,ī”∂ÝĹ‚Ķ√:![]() ,
,
(2)łýĺ›![]() ,ĶĪ
,ĶĪ![]() Ī,Ņ…Ň–∂®ňńĪŖ–őPDBQő™∆Ĺ––ňńĪŖ–ő,łýĺ›∆Ĺ––ňńĪŖ–őĶń–‘÷ Ņ…Ķ√:
Ī,Ņ…Ň–∂®ňńĪŖ–őPDBQő™∆Ĺ––ňńĪŖ–ő,łýĺ›∆Ĺ––ňńĪŖ–őĶń–‘÷ Ņ…Ķ√:![]() ,Ĺ‚Ķ√:
,Ĺ‚Ķ√:![]() ,
,
(3)łýĺ›Ő‚“‚Ņ…Ķ√:![]() ,ĶĪ
,ĶĪ![]() Ī,Ķ„
Ī,Ķ„![]() Ķń◊ÝĪÍő™
Ķń◊ÝĪÍő™![]() ,ĶĪ
,ĶĪ![]() Ī,Ķ„
Ī,Ķ„![]() Ķń◊ÝĪÍő™
Ķń◊ÝĪÍő™![]() ,
,
…Ť÷ĪŌŖ![]() ĶńĹ‚őŲ Ĺő™:
ĶńĹ‚őŲ Ĺő™:![]() ,‘Ú
,‘Ú![]() ,Ĺ‚Ķ√:
,Ĺ‚Ķ√:![]() ,“Úīň÷ĪŌŖ
,“Úīň÷ĪŌŖ![]() ĶńĹ‚őŲ Ĺő™:
ĶńĹ‚őŲ Ĺő™:![]() ,‘Ŕłýĺ›Ő‚“‚Ķ√:Ķ„PĶń◊ÝĪÍő™
,‘Ŕłýĺ›Ő‚“‚Ķ√:Ķ„PĶń◊ÝĪÍő™![]() ,Ķ„QĶń◊ÝĪÍő™
,Ķ„QĶń◊ÝĪÍő™![]() ,“Úīň‘ŕ‘ň∂ĮĻż≥Ő÷–PQĶń÷–Ķ„MĶń◊ÝĪÍő™
,“Úīň‘ŕ‘ň∂ĮĻż≥Ő÷–PQĶń÷–Ķ„MĶń◊ÝĪÍő™![]() ,ĶĪ
,ĶĪ![]() Ī,
Ī,![]() ,“ÚīňĶ„M‘ŕ÷ĪŌŖ
,“ÚīňĶ„M‘ŕ÷ĪŌŖ![]() …Ō,◊ų
…Ō,◊ų![]() ÷Š”ŕN,‘Ú
÷Š”ŕN,‘Ú![]() ,
,![]() ,”…ĻīĻ…∂®ņŪĶ√,
,”…ĻīĻ…∂®ņŪĶ√,![]() ,
,
“ÚīňŌŖ∂őPQ÷–Ķ„Mňýĺ≠ĻżĶń¬∑ĺ∂≥§ő™![]() .
.
![]() ”…Ő‚“‚Ķ√,
”…Ő‚“‚Ķ√,![]() ,
,![]() ,
,
‘Ú![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() °◊
°◊![]() ,
,
![]() ,ľī
,ľī![]() ,
,
Ĺ‚Ķ√:![]() ,
,
Ļ īūįłő™:![]() ,
,![]() ,
,
![]() īś‘ŕ,
īś‘ŕ,
![]() ,
,
![]() ĶĪ
ĶĪ![]() Ī,ňńĪŖ–őPDBQő™∆Ĺ––ňńĪŖ–ő,
Ī,ňńĪŖ–őPDBQő™∆Ĺ––ňńĪŖ–ő,
![]() ,
,
Ĺ‚Ķ√:![]() ,
,
‘ÚĶĪ![]() Ī,ňńĪŖ–őPDBQő™∆Ĺ––ňńĪŖ–ő,
Ī,ňńĪŖ–őPDBQő™∆Ĺ––ňńĪŖ–ő,
![]() “‘Ķ„Cő™‘≠Ķ„,“‘ACňý‘ŕĶń÷ĪŌŖő™x÷Š,Ĺ®ŃĘ»ÁÕľ2ňý ĺĶń∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ,
“‘Ķ„Cő™‘≠Ķ„,“‘ACňý‘ŕĶń÷ĪŌŖő™x÷Š,Ĺ®ŃĘ»ÁÕľ2ňý ĺĶń∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ,
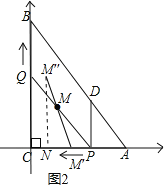
”…Ő‚“‚Ķ√:![]() ,
,
ĶĪ![]() Ī,Ķ„
Ī,Ķ„![]() Ķń◊ÝĪÍő™
Ķń◊ÝĪÍő™![]() ,
,
ĶĪ![]() Ī,Ķ„
Ī,Ķ„![]() Ķń◊ÝĪÍő™
Ķń◊ÝĪÍő™![]() ,
,
…Ť÷ĪŌŖ![]() ĶńĹ‚őŲ Ĺő™:
ĶńĹ‚őŲ Ĺő™:![]() ,
,
‘Ú![]() ,
,
Ĺ‚Ķ√:![]() ,
,
![]() ÷ĪŌŖ
÷ĪŌŖ![]() ĶńĹ‚őŲ Ĺő™£ļ
ĶńĹ‚őŲ Ĺő™£ļ![]() ,
,
”…Ő‚“‚Ķ√:Ķ„PĶń◊ÝĪÍő™![]() ,Ķ„QĶń◊ÝĪÍő™
,Ķ„QĶń◊ÝĪÍő™![]() ,
,
![]() ‘ŕ‘ň∂ĮĻż≥Ő÷–PQĶń÷–Ķ„MĶń◊ÝĪÍő™
‘ŕ‘ň∂ĮĻż≥Ő÷–PQĶń÷–Ķ„MĶń◊ÝĪÍő™![]() ,
,
ĶĪ![]() Ī,
Ī,![]() ,
,
![]() Ķ„M‘ŕ÷ĪŌŖ
Ķ„M‘ŕ÷ĪŌŖ![]() …Ō,
…Ō,
◊ų![]() ÷Š”ŕN,
÷Š”ŕN,
‘Ú![]() ,
,![]() ,
,
”…ĻīĻ…∂®ņŪĶ√,![]() ,
,
![]() ŌŖ∂őPQ÷–Ķ„Mňýĺ≠ĻżĶń¬∑ĺ∂≥§ő™
ŌŖ∂őPQ÷–Ķ„Mňýĺ≠ĻżĶń¬∑ĺ∂≥§ő™![]() .
.



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶxOy÷–£¨“ĽīőļĮ żĶńÕľŌůĺ≠ĻżĶ„A£®2£¨3£©”ŽĶ„B£®0£¨5£©£ģ
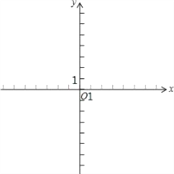
£®1£©«ůīň“ĽīőļĮ żĶńĪŪīÔ Ĺ£Ľ
£®2£©»ŰĶ„Pő™īň“ĽīőļĮ żÕľŌů…Ō“ĽĶ„£¨«“°ųPOBĶń√śĽżő™10£¨«ůĶ„PĶń◊ÝĪÍ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Oő™÷ĪŌŖAB…Ō“ĽĶ„£¨°ŌDOCő™÷ĪĹ«£¨OE∆Ĺ∑÷°ŌAOC£¨OG∆Ĺ∑÷°ŌBOC£¨OF∆Ĺ∑÷°ŌBOD£¨Ō¬Ń–ĹŠ¬ŘīŪőůĶń «£® £©
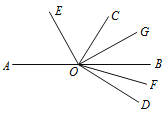
A. °ŌDOG”Ž°ŌBOEĽ•≤Ļ B. °ŌAOE£≠°ŌDOF£Ĺ45°„
C. °ŌEOD”Ž°ŌCOGĽ•≤Ļ D. °ŌAOE”Ž°ŌDOFĽ•”ŗ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ![]() ABCD÷–£¨F «ADĶń÷–Ķ„£¨—”≥§BCĶĹĶ„E£¨ ĻCE=
ABCD÷–£¨F «ADĶń÷–Ķ„£¨—”≥§BCĶĹĶ„E£¨ ĻCE=![]() BC£¨Ń¨ĹŠDE£¨CF°£
BC£¨Ń¨ĹŠDE£¨CF°£

£®1£©«ů÷§£ļňńĪŖ–őCEDF «∆Ĺ––ňńĪŖ–ő£Ľ
£®2£©»ŰAB=4£¨AD=6£¨°ŌB=60°„£¨«ůDEĶń≥§°£
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
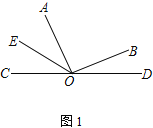
°ĺŐ‚ńŅ°Ņ“—÷™O «÷ĪŌŖ…ŌĶń“ĽĶ„£¨°ŌAOB «÷ĪĹ«£¨OE∆Ĺ∑÷°ŌAOC
(1) ‘ŕÕľĘŔ÷–£¨»Ű°ŌBOD£Ĺ28°„£¨«ů°ŌAOEĶń∂» ż
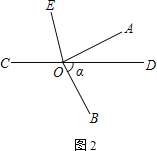
(2) ĹęÕľĘŔ÷–Ķń°ŌAOB»∆∂•Ķ„Oň≥ Ī’Ž–ż◊™÷ŃÕľĘŕĶńőĽ÷√£ģ»Ű°ŌBOD£Ĺ¶Ń£¨ ‘”√ļ¨¶ŃĶń Ĺ◊”ĪŪ ĺ°ŌAOE£¨≤ĘňĶ√ųņŪ”…
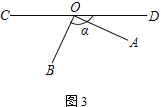
(3) ľŐ–Ý–ż◊™AOB÷ŃÕľĘŘĶńőĽ÷√£¨»Ű°ŌBOD£Ĺ¶Ń£¨∆šňŻŐűľĢ≤ĽĪš£¨ ‘ĹęÕľ–ő≤Ļ≥šÕÍ’Ż£¨«ů°ŌAOEĶń∂» ż.£®”√ļ¨¶ŃĶń Ĺ◊”ĪŪ ĺ£©
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕĶ»—ŁRtABC ÷–£¨°ŌBAC=90°„£¨‘ŕBC…ŌĹō»°BD=BA£¨◊ų°ŌABCĶń∆Ĺ∑÷ŌŖ”ŽADŌŗĹĽ”ŕĶ„P£¨Ń¨Ĺ”PC£¨»Ű°ųABCĶń√śĽżő™8cm2£¨‘Ú°ųBPCĶń√śĽżő™£® £©

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“ĽīőļĮ ży=kx+b£®k°Ŕ0£©”Ž∑īĪ»ņżļĮ ży= ![]() £®m°Ŕ0£©ĶńÕľŌů”–ĻęĻ≤Ķ„A£®1£¨2£©£¨D£®©Ā2£¨©Ā1£©£ģ÷ĪŌŖl°Õx÷Š£¨”Žx÷ŠĹĽ”ŕĶ„N£®3£¨0£©£¨”Ž“ĽīőļĮ żļÕ∑īĪ»ņżļĮ żĶńÕľŌů∑÷ĪūĹĽ”ŕĶ„B£¨C£ģ
£®m°Ŕ0£©ĶńÕľŌů”–ĻęĻ≤Ķ„A£®1£¨2£©£¨D£®©Ā2£¨©Ā1£©£ģ÷ĪŌŖl°Õx÷Š£¨”Žx÷ŠĹĽ”ŕĶ„N£®3£¨0£©£¨”Ž“ĽīőļĮ żļÕ∑īĪ»ņżļĮ żĶńÕľŌů∑÷ĪūĹĽ”ŕĶ„B£¨C£ģ 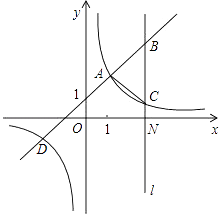
£®1£©«ů“ĽīőļĮ ż”Ž∑īĪ»ņżļĮ żĶńĹ‚őŲ Ĺ£Ľ
£®2£©«ů°ųABCĶń√śĽż£Ľ
£®3£©łýĺ›ÕľŌůĽōīū£¨‘ŕ ≤√ī∑∂őß Ī£¨“ĽīőļĮ żĶń÷Ķīů”ŕ∑īĪ»ņżļĮ żĶń÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨į—“ĽłŲ‘≤◊∂—ōńłŌŖOAľŰŅ™£¨’ĻŅ™ļůĶ√ĶĹ…»–őAOC£¨“—÷™‘≤◊∂ĶńłŖhő™12cm£¨OA=13cm£¨‘Ú…»–őAOC÷– ![]() Ķń≥§ «cm£®ľ∆ň„ĹŠĻŻĪ£Ń۶–£©£ģ
Ķń≥§ «cm£®ľ∆ň„ĹŠĻŻĪ£Ń۶–£©£ģ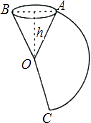
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
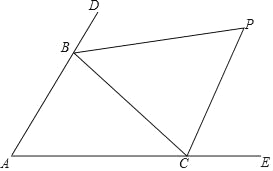
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨°ųABC÷–£¨∑÷Īū—”≥§°ųABCĶńĪŖAB°ĘACĶĹD°ĘE£¨°ŌCBD”Ž°ŌBCEĶń∆Ĺ∑÷ŌŖŌŗĹĽ”ŕĶ„P£¨įģ∂Įń‘ĹÓĶń–°√ų‘ŕ–ī◊ų“ĶĶń Ī∑ĘŌ÷»ÁŌ¬Ļś¬…£ļ
(1)»Ű°ŌA£Ĺ60°„£¨‘Ú°ŌP£Ĺ°° °°°„£Ľ
(2)»Ű°ŌA£Ĺ40°„£¨‘Ú°ŌP£Ĺ°° °°°„£Ľ
(3)»Ű°ŌA£Ĺ100°„£¨‘Ú°ŌP£Ĺ°° °°°„£Ľ
(4)«Žń„”√ ż—ßĪŪīÔ ĹĻťń…°ŌA”Ž°ŌPĶńĻōŌĶ°° °°£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com