
【题目】已知abc ![]() 0,而且
0,而且 ![]() ,那么直线y=px+p一定通过( )
,那么直线y=px+p一定通过( )
A.第一、二象限
B.第二、三象限
C.第三、四象限
D.第一、四象限
【答案】B
【解析】由条件得:①a+b=pc , ②b+c=pa , ③a+c=pb ,
三式相加得2(a+b+c)=p(a+b+c).
∴有p=2或a+b+c=0.
当p=2时,y=2x+2.则直线通过第一、二、三象限.
当a+b+c=0时,不妨取a+b=-c , 于是p= ![]() =-1,(c≠0),
=-1,(c≠0),
∴y=-x-1,
∴直线通过第二、三、四象限.
综合上述两种情况,直线一定通过第二、三象限.
答案为:B.
【考点精析】认真审题,首先需要了解一次函数的图象和性质(一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远),还要掌握比例的性质(基本性质;更比性质(交换比例的内项或外项);反比性质(交换比的前项、后项);等比性质)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,OA=8,OB=6,C点与A点关于直线OB对称,动点P、Q分别在线段AC、AB上(点P不与点A.C重合),满足∠BPQ=∠BAO.
(1)当OP=_______时,△APQ≌△CBP,说明理由;
(2)当△PQB为等腰三角形时,求OP的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
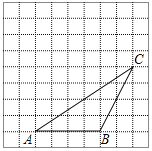
【题目】如图,在每个小正方形边长为1的方格纸中,△ADC的顶点都在方格纸格点上,将△ABC向左平移1格.再向上平移1格,
(1)在图中画出平移后的△A′B′C′;
(2)画出AB边上的高CE;
(3)过点A画BC的平行线;
(4)在图中,若△BCQ的面积等于△BCA的面积.则图中满足条件且异于点A的个点Q共有_____个.(注:格点指网格线的交点)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°, AB//CD,M为BC边上的一点,AM平分∠BAD,DM平分∠ADC,
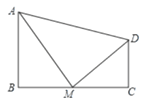
求证:(1) AM⊥DM;
(2) M为BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
如:P(1,4)的“2属派生点为P′(1+2×4,2×1+4),即P′(9,6);
(1)点P(-1,3)的“2属派生点”P′的坐标为______;
(2)若点P的“3属派生点”P′的坐标为(-1,3),则点P的坐标为______.
(3)若点P在x轴的正半轴上,点P的“k属派生点”为点P′,线段PP′的长度等于线段OP的长度,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD。过点D作DE⊥AB于E,交AC于点P,求证:点P平分线段DE。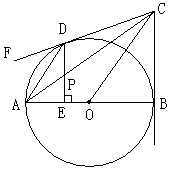
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
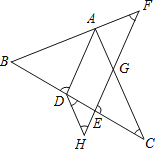
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,若∠F=40°,求∠H的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
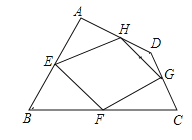
(1)四边形EFGH的形状是 ,证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com