
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
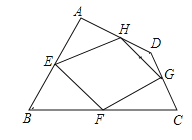
(1)四边形EFGH的形状是 ,证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? .
【答案】(1)平行四边形,证明见解析.
(2)四边形ABCD的对角线满足互相垂直,证明见解析,
(3)菱形,证明见解析.
【解析】
(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=![]() BD,FG∥BD,FG═
BD,FG∥BD,FG═![]() BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
(3)菱形的中点四边形是矩形.根据三角形的中位线平行于第三边并且等于第三边的一半可得四边形EFGH是平行四边形,再根据矩形的每一个角都是直角,然后根据平行线的性质,再根据垂直定义解答;
解:(1)四边形EFGH的形状是平行四边形.理由如下:
如图,连结BD. ∵E、H分别是AB、AD中点,
∴EH∥BD,EH= ![]() BD,
BD,
同理FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
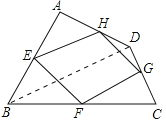
故答案为:平行四边形.
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.
理由如下: 如图,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD, ∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
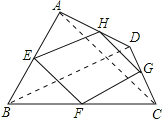
故答案为:对角线互相垂直.
(3)菱形的中点四边形是矩形.
理由如下: 如图,连结AC、BD. ∵E、F、G、H分别为四边形ABCD四条边上的中点, ∴EH∥BD,HG∥AC,FG∥BD,EH=![]() BD,FG=
BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH是矩形;
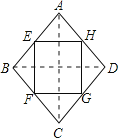
故答案为:菱形.


科目:初中数学 来源: 题型:
【题目】某景点的门票价格规定如下表:
我校初二(1),(2)两个班共104人准备利用假期去游览该景点,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人,经估算,如果两班都以班为单位分别购票,则一共应付1240元,问两班各有多少名学生? 你认为还有没有好的方法去节省门票的费用?若有,请按照你的方法计算一下能省多少钱?(
购票人数 | 1-50人 | 51-100人 | 100人以上 |
每人门票价 | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2 ![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H
(1) 求证:HE=HG
(2) 如图2,当BE=AB时,过点A作AP⊥DE于点P连接BP,求![]() 的值
的值
(3) 在(2)的条件下,若AD=2,∠ADE=30°,则BP的长为______________


查看答案和解析>>
科目:初中数学 来源: 题型:
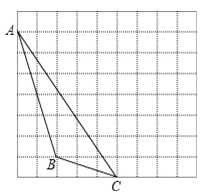
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上
(1)画出△ABC向右平移4格, 再向上平移1格后的△A1B1C1;
(2)图中BC与B1C1的关系是 ;
(3)图中△ABC的面积是
(4)请在AB上找一点D,使得线段CD平分△ABC的面积,在图上作出线段CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D. 
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,做直线AE,且∠EAC=∠D 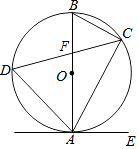
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD= ![]() ,CF=
,CF= ![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com