
【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,做直线AE,且∠EAC=∠D 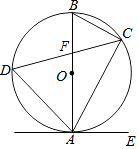
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD= ![]() ,CF=
,CF= ![]() ,求BF的长.
,求BF的长.
【答案】
(1)证明:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
即∠ADC+∠CDB=90°,
∵∠EAC=∠ADC,∠CDB=∠BAC,
∴∠EAC+∠BAC=90°,
即∠BAE=90°,
∴直线AE是⊙O的切线;
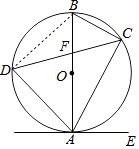
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
Rt△ACB中,∠BAC=30°,
∴AB=2BC=2×4=8,
由勾股定理得:AC= ![]() =4
=4 ![]() ,
,
Rt△ADB中,cos∠BAD= ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴AD=6,
∴BD= ![]() =2
=2 ![]() ,
,
∵∠BDC=∠BAC,∠DFB=∠AFC,
∴△DFB∽△AFC,
∴ ![]() ,
,
∴ ![]() ,
,
∴BF= ![]() .
.
【解析】(1)由直径所对的圆周角是直角得:∠ADB=90°,则∠ADC+∠CDB=90°,所以∠EAC+∠BAC=90°,则直线AE是⊙O的切线;(2)分别计算AC和BD的长,证明△DFB∽△AFC,列比例式得: ![]() ,得出结论.
,得出结论.
【考点精析】利用解直角三角形对题目进行判断即可得到答案,需要熟知解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
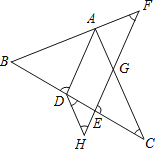
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,若∠F=40°,求∠H的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
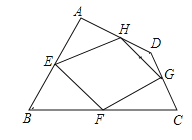
(1)四边形EFGH的形状是 ,证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵![]() 两次共花费940元
两次共花费940元![]() 两次购进的A、B两种花草价格均分别相同
两次购进的A、B两种花草价格均分别相同![]() .
.
![]() 、B两种花草每棵的价格分别是多少元?
、B两种花草每棵的价格分别是多少元?
![]() 若再次购买A、B两种花草共12棵
若再次购买A、B两种花草共12棵![]() 、B两种花草价格不变
、B两种花草价格不变![]() ,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市是蜜桔之乡,今年桔子大丰收,某合作社要把240吨桔子运往某市的A、B两地,用大、小两种货车共20辆,恰好能一次性运完这批桔子,已知这两种货车的载重量分别为15吨/辆和10吨/辆.
(1)这两种货车各有多少辆?
(2)运往A地的运费为:大车630元/辆,小车420元/辆;运往B地的运费为:大车750元/辆,小车550元/辆.若把20辆货车中的10辆安排前往A地,其余货车前往B地,其中调往A地的大车有a辆,求总运费.(用含a的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于
中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于![]() 轴的对称点为B′,点C关于
轴的对称点为B′,点C关于![]() 轴的对称点为C′.
轴的对称点为C′.
(1)A′的坐标为 ,B′的坐标为 ,C′的坐标为 .
(2)建立平面直角坐标系,描出以下三点A、B′、C′,并求△AB′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰三角形的腰长为6cm,底边长为4cm,以等腰三角形的顶角的顶点为圆心5cm为半径画圆,那么该圆与底边的位置关系是( )
A.相离
B.相切
C.相交
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在解方程组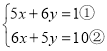 时,我们可以先①+②,得
时,我们可以先①+②,得![]() 再②-①,得
再②-①,得![]() 最后重新组成方程组
最后重新组成方程组![]() ,这种解二元一次方程组的解法我们称为二元一次方程组的轮换对称解法.
,这种解二元一次方程组的解法我们称为二元一次方程组的轮换对称解法.
(1)用轮换对称解法解方程组![]() ,得_____________________________;
,得_____________________________;
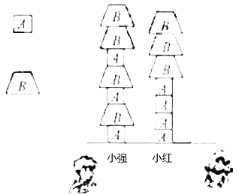
(2)如图,小强和小红一起搭积木,小强所搭的“小塔”高度为32cm,小红所搭的“小树”高度为3lcm,设每块A型积木的高为![]() 每块B型积木的高为
每块B型积木的高为![]() 求
求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com