
【题目】在平面直角坐标系![]() 中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于
中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于![]() 轴的对称点为B′,点C关于
轴的对称点为B′,点C关于![]() 轴的对称点为C′.
轴的对称点为C′.
(1)A′的坐标为 ,B′的坐标为 ,C′的坐标为 .
(2)建立平面直角坐标系,描出以下三点A、B′、C′,并求△AB′C′的面积.
【答案】(1)(1,-5),(4,-2)、(1,0);(2)图详见解析,7.5 .
【解析】
(1)关于原点对称的两点的横、纵坐标都是互为相反数;关于x轴对称的两点的横坐标相同,纵坐标互为相反数;关于y轴对称的两点的横坐标互为相反数,纵坐标相同;
(2)根据点A′(1,-5),B′(4,-2),C′(1,0)在平面直角坐标系中的位置,可以求得A′C′=5,B′D=3,所以由三角形的面积公式进行解答.
解:(1)∵A(-1,5),
∴点A关于原点O的对称点A′的坐标为(1,-5).
∵B(4,2),
∴点B关于x轴的对称点B′的坐标为(4,-2).
∵C(-1,0),
∴点C关于y轴的对称点C′的坐标为(1,0).
故答案为:(1,-5),(4,-2),(1,0).
(2)如图,
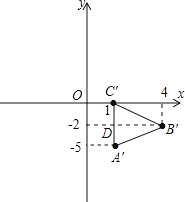
∵A′(1,-5),B′(4,-2),C′(1,0).
∴A′C′=|-5-0|=5,B′D=|4-1|=3,
![]() ,即△A′B′C′的面积是7.5.
,即△A′B′C′的面积是7.5.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
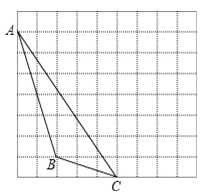
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上
(1)画出△ABC向右平移4格, 再向上平移1格后的△A1B1C1;
(2)图中BC与B1C1的关系是 ;
(3)图中△ABC的面积是
(4)请在AB上找一点D,使得线段CD平分△ABC的面积,在图上作出线段CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC. 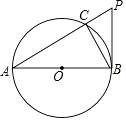
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,做直线AE,且∠EAC=∠D 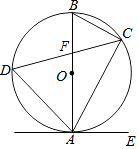
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD= ![]() ,CF=
,CF= ![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中,∠C=90°,BC=1,AC=![]() ,点D是斜边AB的中点,点E是边AC上一点,则DE+BE的最小值为( )
,点D是斜边AB的中点,点E是边AC上一点,则DE+BE的最小值为( )

A. 2
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.

(1)求∠EOB的度数.
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化? 若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA? 若存在,求出∠OBA的度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
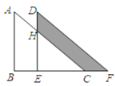
【题目】如图,将直角三角形ABC沿着BC方向平移![]() cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.
cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com