
【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC. 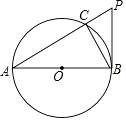
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
【答案】
(1)解:∵AB是⊙O的直径,PB与⊙O相切于点B,
∴∠ACB=∠ABP=90°,
∴∠A+∠ABC=∠ABC+∠CBP=90°,
∴∠BAC=∠CBP
(2)解:∵∠PCB=∠ABP=90°,
∠P=∠P,
∴△ABP∽△BCP,
∴ ![]() ,
,
∴PB2=PCPA
(3)解:∵PB2=PCPA,AC=6,CP=3,
∴PB2=9×3=27,
∴PB=3 ![]() ,
,
∴sin∠PAB= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)根据已知条件得到∠ACB=∠ABP=90°,根据余角的性质即可得到结论;(2)根据相似三角形的判定和性质即可得到结论;(3)根据三角函数的定义即可得到结论.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9
(1)求证:△COD∽△CBE;
(2)求半圆O的半径 ![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD. 
(1)求证:△ACD∽△BAD;
(2)求证:AD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E. 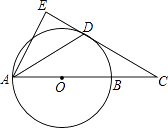
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3 ![]() ,求弦AD的长.
,求弦AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵![]() 两次共花费940元
两次共花费940元![]() 两次购进的A、B两种花草价格均分别相同
两次购进的A、B两种花草价格均分别相同![]() .
.
![]() 、B两种花草每棵的价格分别是多少元?
、B两种花草每棵的价格分别是多少元?
![]() 若再次购买A、B两种花草共12棵
若再次购买A、B两种花草共12棵![]() 、B两种花草价格不变
、B两种花草价格不变![]() ,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C、D、E、F六个球队进行单循环比赛(每两队之间赛一场,比赛结果必须分出胜负),每天同时在三个场地各进行一场比赛,前四天的积分表如下(E、F的积分被遮挡):
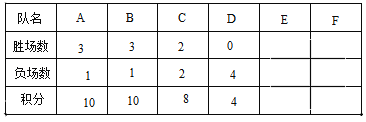
(1)根据积分榜,胜一场积几分,负一场积几分?
(2)若E队前四天积分比F队多4分,问E、F两队前四天的战绩分别是几胜几负?
(3)已知第一天B与D对阵,第二天C与E对阵,第三天D与F对阵,第四天B与C对阵,试分析第五天A和谁对阵比赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于
中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于![]() 轴的对称点为B′,点C关于
轴的对称点为B′,点C关于![]() 轴的对称点为C′.
轴的对称点为C′.
(1)A′的坐标为 ,B′的坐标为 ,C′的坐标为 .
(2)建立平面直角坐标系,描出以下三点A、B′、C′,并求△AB′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发区在一项工程招标时,接到甲、乙两个工程队的投标书,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:①甲队单独完成这项工程,刚好如 期完成;②乙队单独完成此项工程要比规定工期多用5天;③ ![]() ,剩下的工程由乙队单独做,也正好如期完工.小亮设规定的工期为x天,根据题意列出了方 程:
,剩下的工程由乙队单独做,也正好如期完工.小亮设规定的工期为x天,根据题意列出了方 程: ![]() ,则方案③中被墨水污染的部分应该是( )
,则方案③中被墨水污染的部分应该是( )
A.甲先做了4天
B.甲乙合作了4天
C.甲先做了工程的 ![]()
D.甲乙合作了工程的 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
(1)如图1,∠BME,∠E,∠END的数量关系为 (直接写出答案);
(2)如图2,∠BME=m°,EF平分∠MEN,NP平分∠END,EQ∥NP,求∠FEQ的度数(用用含m的式子表示)
(3)如图3,点G为CD上一点,∠BMN=n·∠EMN,∠GEK=n·∠GEM,EH∥MN交AB于点H,探究∠GEK,∠BMN,∠GEH之间的数量关系(用含n的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com