
【题目】如图,将矩形![]() 沿直线
沿直线![]() 折叠,顶点
折叠,顶点![]() 恰好落在
恰好落在![]() 边上
边上![]() 点处,已知
点处,已知![]() ,则图中阴影部分面积为( )
,则图中阴影部分面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根据折叠的性质求出DE=EF=5,在Rt△CEF中,利用勾股定理求出CF=4,设AD=x,则AD=AF=BC=x,在Rt△ABF中,利用勾股定理构建方程即可解决问题.
解:设AD=x,则AD=AF=BC=x,
∵AB=8,
∴CD=AB=8,
∵CE=3,
∴EF=DE=CD﹣CE=8﹣3=5,
在直角△CEF中,CF=![]() =4,
=4,
∴BF=x﹣4,
在直角△ABF中,AB2+BF2=AF2,即64+(x﹣4)2=x2,
解得:x=10,
∴S△ADE=S△AFE=![]() ADDE=
ADDE=![]() ×10×5=25,
×10×5=25,
∵S矩形ABCD=10×8=80,
∴S阴影=S矩形ABCD﹣S△ADE﹣S△AFE=80﹣25﹣25=30.
故选:C.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】某景点的门票价格规定如下表:
我校初二(1),(2)两个班共104人准备利用假期去游览该景点,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人,经估算,如果两班都以班为单位分别购票,则一共应付1240元,问两班各有多少名学生? 你认为还有没有好的方法去节省门票的费用?若有,请按照你的方法计算一下能省多少钱?(
购票人数 | 1-50人 | 51-100人 | 100人以上 |
每人门票价 | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D. 
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,做直线AE,且∠EAC=∠D 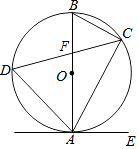
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD= ![]() ,CF=
,CF= ![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() 、
、![]() ,连接
,连接![]() .如果点
.如果点![]() 在直线
在直线![]() 上,且点
上,且点![]() 到直线
到直线![]() 的距离不大于1,那么称点
的距离不大于1,那么称点![]() 是线段
是线段![]() 的“临近点”.
的“临近点”.

(1)判断点![]() 是否是线段
是否是线段![]() 的“临近点”,并说明理由;
的“临近点”,并说明理由;
(2)若点![]() 是线段
是线段![]() 的“临近点”.①求
的“临近点”.①求![]() 的取值范围;②设直线
的取值范围;②设直线![]() 与
与![]() 轴交于
轴交于![]() 点,试用
点,试用![]() 表达
表达![]() 的面积
的面积![]() ,并求出
,并求出![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.

(1)求∠EOB的度数.
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化? 若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA? 若存在,求出∠OBA的度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-a3·a4;
(2) ![]() 2018×
2018×![]() 2019.
2019.
(3)(-2x2y)3·3(xy2)2;
(4)(-3a+2b)2
(5)(x-2)(x+2)(x2+4).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( ) 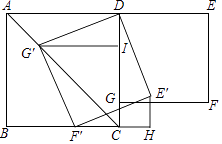
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com