
����Ŀ��ijѧУΪ���ư�ѧ�������ƻ��ɹ�A��B�����ͺŵĿյ�����֪�ɹ�3̨A�Ϳյ���2̨B�Ϳյ��������39000Ԫ��4̨A�Ϳյ���5̨B�Ϳյ��ķ��ö�6000Ԫ��
��1����A�Ϳյ���B�Ϳյ�ÿ̨�������Ԫ��
��2����ѧУ�ƻ��ɹ�A��B�����ͺſյ���30̨����A�Ϳյ���̨��������B�Ϳյ���һ�룬�����ͺſյ��IJɹ��ܷ��ò�����217000Ԫ����У�����ļ��ֲɹ�������
��3���ڣ�2���������£�������һ�ֲɹ�������ʹ�ܷ�����ͣ���ͷ����Ƕ���Ԫ��
���𰸡���1��A�Ϳյ���B�Ϳյ�ÿ̨����9000Ԫ��6000Ԫ����2���������ֲɹ�����������һ���ɹ�A�Ϳյ�10̨��B�Ϳյ�20̨�����������ɹ�A�Ϳյ�11̨��B�Ϳյ�19̨���������ɹ�A�Ϳյ�12̨��B�Ϳյ�18̨����3���ɹ�A�Ϳյ�10̨��B�Ϳյ�20̨��ʹ�ܷ�����ͣ���ͷ�����210000Ԫ��
����������1��������������г���Ӧ�ķ����飬�Ӷ����Խ���⣻
��2��������������г���Ӧ�IJ���ʽ�飬�Ӷ���������м��ֲɹ�������
��3����������ͣ�2���еĽ�������Խ���⣮
��1����A�Ϳյ���B�Ϳյ�ÿ̨����xԪ��yԪ��
![]() ����ã�
����ã�![]() ��
��
��A�Ϳյ���B�Ϳյ�ÿ̨����9000Ԫ��6000Ԫ��
��2���蹺��A�Ϳյ�ą������B�Ϳյ���30-a��̨��
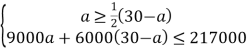 ��
��
��ã�10��a��12![]() ��
��
��a=10��11��12���������ֲɹ�������
����һ���ɹ�A�Ϳյ�10̨��B�Ϳյ�20̨��
���������ɹ�A�Ϳյ�11̨��B�Ϳյ�19̨��
���������ɹ�A�Ϳյ�12̨��B�Ϳյ�18̨��
��3�����ܷ���ΪwԪ��
w=9000a+6000��30-a��=3000a+180000��
�൱a=10ʱ��wȡ����Сֵ����ʱw=210000��
���ɹ�A�Ϳյ�10̨��B�Ϳյ�20̨��ʹ�ܷ�����ͣ���ͷ�����210000Ԫ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ı���ABCD�������ϵ��е�ֱ�ΪE��F��G��H��˳������EF��FG��GH��HE���õ��ı���EFGH�����ı���ABCD���е��ı��Σ���
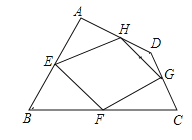
��1���ı���EFGH����״�� ��֤����Ľ��ۣ�
��2�����ı���ABCD�ĶԽ������� ����ʱ���ı���EFGH�Ǿ��Σ�
��3����ѧ�������������ı��ε��е��ı����Ǿ��Σ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��ֱ��
��ֱ��![]() �۵�������
�۵�������![]() ǡ������
ǡ������![]() ����
����![]() �㴦����֪
�㴦����֪![]() ����ͼ����Ӱ�������Ϊ�� ��
����ͼ����Ӱ�������Ϊ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ε�����Ϊ6cm���ױ߳�Ϊ4cm���Ե��������εĶ��ǵĶ���ΪԲ��5cmΪ�뾶��Բ����ô��Բ��ױߵ�λ�ù�ϵ�ǣ� ��
A.����
B.����
C.�ཻ
D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ο�ƬA�ࡢB��ͳ����ο�ƬC��������ţ����Ҫƴһ����Ϊ(a��3b)����Ϊ(2a��b)�Ĵ��Σ�
��1����ҪA�ࡢB���C�Ƭ�������ֱ�Ϊ(����)��
A��2,3,7�� B��3,7,2
C��2,5,3�� D��2,5,7
��2������������.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��bx��c�У��Ա���x�뺯��y֮��IJ��ֶ�Ӧֵ���±���
�ڸú�����ͼ������A��x1 �� y1����B��x2 �� y2�����㣬��-1��x1��0��3��x2��4��y1��y2�Ĵ�С��ϵ��ȷ���ǣ� ��
A.y1��y2
B.y1��y2
C.y1��y2
D.y1��y2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+2x+3��x�ύ��A��B���㣬��y�ύ��C�㣬�Գ������������ཻ�ڵ�M����x���ཻ�ڵ�N����P���߶�MN�ϵ�һ���㣬����P��PE��CP��x���ڵ�E��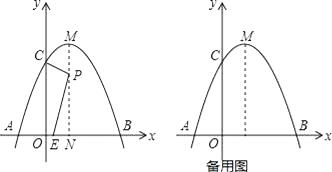
��1��ֱ��д�������ߵĶ���M�������� ��
��2������E���O��ԭ�㣩�غ�ʱ�����P�����꣮
��3����P��M�˶���N�Ĺ����У���E���˶���·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������:�ڽⷽ����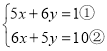 ʱ�����ǿ����Ȣ�+�ڣ���
ʱ�����ǿ����Ȣ�+�ڣ���![]() �٢�-�٣���
�٢�-�٣���![]() ���������ɷ�����
���������ɷ�����![]() �����ֽ��Ԫһ�η�����Ľⷨ���dz�Ϊ��Ԫһ�η�������ֻ��Գƽⷨ.
�����ֽ��Ԫһ�η�����Ľⷨ���dz�Ϊ��Ԫһ�η�������ֻ��Գƽⷨ.
(1)���ֻ��Գƽⷨ�ⷽ����![]() ����_____________________________��
����_____________________________��
(2)��ͼ��Сǿ��С��һ����ľ��Сǿ�������С�����߶�Ϊ32cm��С���������С�����߶�Ϊ3lcm����ÿ��A�ͻ�ľ�ĸ�Ϊ![]() ÿ��B�ͻ�ľ�ĸ�Ϊ
ÿ��B�ͻ�ľ�ĸ�Ϊ![]() ��
��![]() ��
��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
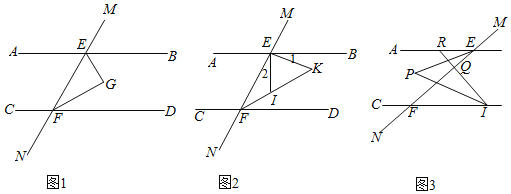
����Ŀ����֪��ֱ��AB��CD��ֱ��MN�ֱ���AB��CD���ڵ�E��F��
��1����ͼ1����BEF�͡�EFD��ƽ���߽��ڵ�G�����G�Ķ�����
��2����ͼ2��EI��EKΪ��BEF�������1����2�������ߣ��ֱ����EFD��ƽ���߽��ڵ�I��K�������FIE�͡�K�Ĺ�ϵ����֤����
��3����ͼ3����QΪ�߶�EF���˵���⣩�ϵ�һ�����㣬����Q��EF�Ĵ��߽�AB��R����CD��J����AEF����CJR��ƽ�����ཻ��P���ʡ�EPJ�Ķ����Ƿ�ᷢ���仯�����������仯�������EPJ�Ķ��������ᷢ���仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com