
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.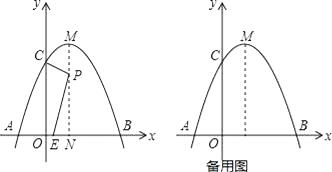
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长.
【答案】
(1)M(1,4)
(2)解:当点E与O重合时,EN=1,设PN=m,
过点C作CF⊥MN,垂足为F,如图1,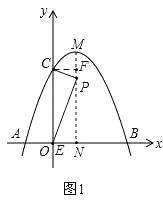
∵∠EPC=90°,
∴∠EPN+∠NEP=∠EPN+∠CPF=90°,
∴∠CPF=∠PEN,
∴△ENP∽△PFC
∴ ![]() ,即:
,即: ![]() ,
,
解得:m= ![]()
∴点P的坐标为:(1, ![]() )或(1,
)或(1, ![]() )
)
(3)解:①当点P与M重合时,如图2,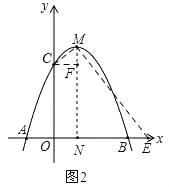
由△ENM∽△MFC可知, ![]() ,
,
∴EN=4,
即当点P从M运动到F时,点E运动的路径长EN为4;
②当点P从F运动到N时,点E从点N向左运动到某最远点后,回到点N结束.如图3,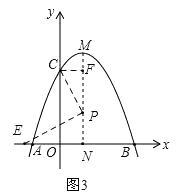
设EN=y,PN=x,
由△ENP∽△PFC可知, ![]() ,即:
,即: ![]() ,
,
∴y= ![]() ,
,
当x= ![]() 时,y有最大值,为
时,y有最大值,为 ![]() ;
;
∴E的运动的路径长为: ![]() .
.
【解析】抛物线的顶点M的坐标是M(1,4)


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D. 
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-a3·a4;
(2) ![]() 2018×
2018×![]() 2019.
2019.
(3)(-2x2y)3·3(xy2)2;
(4)(-3a+2b)2
(5)(x-2)(x+2)(x2+4).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°.将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1 , B1C1交AC于点D,如果AD=2 ![]() ,则△ABC的周长等于 .
,则△ABC的周长等于 . 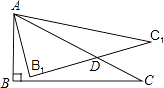
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( ) 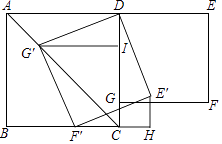
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=25°,∠ADC=115°,O为AB的中点,以点O为圆心、AO长为半径作圆,恰好点D在⊙O上,连接OD,若∠EAD=25°,下列说法中不正确的是( ) 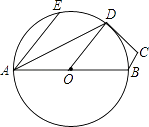
A.D是劣弧 ![]() 的中点
的中点
B.CD是⊙O的切线
C.AE∥OD
D.∠DOB=∠EAD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com