练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为(a＋3b)、宽为(2a＋b)的大长方形；

    （1）需要A类、B类和C类卡片的张数分别为(　　)；

    A．2,3,7　 B．3,7,2

    C．2,5,3　 D．2,5,7

    （2）画出长方形.

    【答案】（1）A；（2）见解析.

    【解析】

    （1）根据长方形的面积=长×宽，求出长为a+3b，宽为2a+b的大长方形的面积是多少，判断出需要A类、B类、C类卡片各多少张即可；

    （2）依题意，画出长方形即可.

    （1）长为a+3b，宽为2a+b的长方形的面积为：（a+3b）（2a+b）=2a2+7ab+3b2，

    ∵A类卡片的面积为a2，B类卡片的面积为b2，C类卡片的面积为ab，

    ∴需要A类卡片2张，B类卡片3张，C类卡片7张．

    故选：A；

    （2）画长方形如图：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形ABCD中，E是CB延长线上一个动点，F、G分别为AE、BC的中点，FG与ED相交于点H

    (1) 求证：HE＝HG

    (2) 如图2，当BE＝AB时，过点A作AP⊥DE于点P连接BP，求的值

    (3) 在(2)的条件下，若AD＝2，∠ADE＝30°，则BP的长为______________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点、，连接.如果点在直线上，且点到直线的距离不大于1，那么称点是线段的“临近点”.

    （1）判断点是否是线段的“临近点”，并说明理由；

    （2）若点是线段的“临近点”.①求的取值范围；②设直线与轴交于点，试用表达的面积，并求出的最大面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    (1)－a3·a4；

    (2) 2018×2019.

    (3)(－2x2y)3·3(xy2)2；

    (4)(－3a＋2b)2

    (5)(x－2)(x＋2)(x2＋4)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探索平方差公式的几何背景

    如图1，边长为a的大正方形中有一个边长为b的小正方形．

    (1)请表示图中阴影部分的面积： ；

    (2)小颖将阴影部分拼成了一个长方形(如图2)，这个长方形的长和宽分别是 ，它的面积是 ；

    (3)比较(1)(2)的结果，你能验证平方差公式吗？说一说验证的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校为改善办学条件，计划采购A、B两种型号的空调，已知采购3台A型空调和2台B型空调，需费用39000元；4台A型空调比5台B型空调的费用多6000元．

    （1）求A型空调和B型空调每台各需多少元；

    （2）若学校计划采购A、B两种型号空调共30台，且A型空调的台数不少于B型空调的一半，两种型号空调的采购总费用不超过217000元，该校共有哪几种采购方案？

    （3）在（2）的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于 的方程 的解是 = ， = （ 、 、 为常数， 0），则方程 的解是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ABC=90°，∠ACB=30°．将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1 ， B1C1交AC于点D，如果AD=2 ，则△ABC的周长等于 ．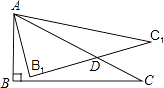

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ABC=90°，AB=BC= ，将△ABC绕点C逆时针旋转60°，得到△MNC，连接BM，则BM的长是

    查看答案和解析>>

    同步练习册答案