
【题目】探索平方差公式的几何背景
如图1,边长为a的大正方形中有一个边长为b的小正方形.
(1)请表示图中阴影部分的面积: ;
(2)小颖将阴影部分拼成了一个长方形(如图2),这个长方形的长和宽分别是 ,它的面积是 ;

(3)比较(1)(2)的结果,你能验证平方差公式吗?说一说验证的理由.
【答案】(1) a2-b2;(2)这个长方形的长和宽分别是a+b,a-b,它的面积是(a+b)(a-b);(2)能.理由:阴影部分的面积是不变的,即(a+b)(a-b)=a2-b2.
【解析】
(1)求出大正方形及小正方形的面积,作差即可得出阴影部分的面积;
(2)图乙所示的长方形的长和宽分别为(a+b)、(a-b),由此可计算出面积;
(3)根据阴影部分的面积相等可得出平方差公式.
(1)大正方形的面积为a2,小正方形的面积为b2,
故图甲阴影部分的面积值为a2-b2;
(2)长方形的长和宽分别为(a+b)、(a-b),
故重拼的长方形的面积为(a+b)(a-b);
(3)比较(1)和(2)的结果,都表示同一阴影的面积,它们相等,
即a2-b2=(a+b)(a-b),可以验证平方差公式,这也是平方差公式的几何意义.


科目:初中数学 来源: 题型:
【题目】学校利用五一组织老师去娄山关进行红色文化拓展活动,现有甲、乙两家旅行 社可供选择,票价都是![]() 元/人,甲旅行社的优惠方案是:按总价打八五折;乙旅行社 的优惠方案是:前
元/人,甲旅行社的优惠方案是:按总价打八五折;乙旅行社 的优惠方案是:前![]() 人按原价付费,超过的部分
人按原价付费,超过的部分![]() 折优惠.该校有教师
折优惠.该校有教师![]() 人.
人.
(1)设总价为![]() 元.写出
元.写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在不晓得该校人数的情况下,请给学校提出比较省钱的购票建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.

(1)猜想四边形PCOB是什么四边形,并说明理由;
(2)当矩形ABCD满足什么条件时,四边形PCOB是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.
(1)求这种笔和本子的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为(a+3b)、宽为(2a+b)的大长方形;
(1)需要A类、B类和C类卡片的张数分别为( );
A.2,3,7 B.3,7,2
C.2,5,3 D.2,5,7
(2)画出长方形.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两艘专业救援船A,B同时收到信息,前往被困船只C所在海域实施救援任务,被困船只C位于救援船A的北偏东60°的方向上,位于救援船B的北偏西30°的方向上,船B在船A正东方向120海里处.
(1)求被困船只C到A、B两船所在直线的距离;
(2)若救援船A,救援船B分别以60海里/时,50海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达C处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是面积为 ![]() 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号). 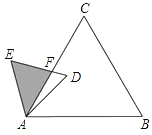
查看答案和解析>>
科目:初中数学 来源: 题型:
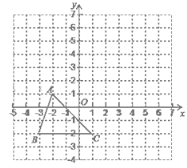
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′、C′的坐标;
(2)求出△ABC的面积;
(3)点P在y轴上,且△BCP是△ABC的面积的2倍,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com