
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
如:P(1,4)的“2属派生点为P′(1+2×4,2×1+4),即P′(9,6);
(1)点P(-1,3)的“2属派生点”P′的坐标为______;
(2)若点P的“3属派生点”P′的坐标为(-1,3),则点P的坐标为______.
(3)若点P在x轴的正半轴上,点P的“k属派生点”为点P′,线段PP′的长度等于线段OP的长度,求k的值.
【答案】(1)(5,1);(2)(![]() ,
,![]() );(3)k=±1.
);(3)k=±1.
【解析】
(1)根据“k属派生点”计算可得;
(2)设点P的坐标为(x、y),根据“k属派生点”定义及P′的坐标列出关于x、y的方程组,解之可得;
(3)先得出点P′的坐标为(a,ka),由线段PP′的长度为线段OP长度的2倍列出方程,解之可得.
(1)点P(-1,3)的“2属派生点”P′的坐标为(-1+3×2,-1×2+3),即(5,1),
故答案为:(5,1),
(2)设P(x,y),
依题意,得方程组:![]() ,
,
解得 ,
,
∴点P(![]() ,
,![]() ).
).
故答案是:(![]() ,
,![]() ).
).
(3)∵点P(a,b)在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka),
∴线段PP′的长为点P′到x轴距离为|ka|,
∵P在x轴正半轴,线段OP的长为a,
根据题意,有|PP'|=|OP|,
∴|ka|=a,
∵a>0,
∴|k|=1.
从而k=±1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB边中点,点E是BC边上一点,将△ADE沿DE折叠,得到△FDE,使△FDE与△BDE重叠部分的面积是△AEB面积的![]() ,若AC=3,BC=6,则线段BE的长为__________.
,若AC=3,BC=6,则线段BE的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠B=50°,P 是边 AB 上的一个动点(不与顶点 A 重合),则∠BPC 的度数可能是

A. 50° B. 80° C. 100° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料
已知:如图,四边形ABCD是平行四边形;
求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(1)连接AC;
(2)作AC的垂直平分线EF分别交BC,AD于E,F.
(3)连接AE,CF
所以四边形AECF是菱形.
老师说:“小凯的作法正确”.
回答问题:
已知:在平行四边形ABCD中,点E、F分别在边BC、AD上______________________________________________.(补全已知条件)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请![]() 个好友转发,每个好友转发之后,又邀请
个好友转发,每个好友转发之后,又邀请![]() 个互不相同的好友转发,已知经过两轮转发后,共有
个互不相同的好友转发,已知经过两轮转发后,共有![]() 个 人参与了本次活动.
个 人参与了本次活动.
(1)x的值是多少?
(2)再经过几轮转发后,参与人数会超过![]() 人?
人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
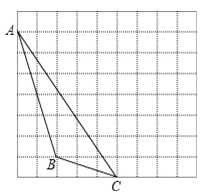
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上
(1)画出△ABC向右平移4格, 再向上平移1格后的△A1B1C1;
(2)图中BC与B1C1的关系是 ;
(3)图中△ABC的面积是
(4)请在AB上找一点D,使得线段CD平分△ABC的面积,在图上作出线段CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com