
【题目】为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请![]() 个好友转发,每个好友转发之后,又邀请
个好友转发,每个好友转发之后,又邀请![]() 个互不相同的好友转发,已知经过两轮转发后,共有
个互不相同的好友转发,已知经过两轮转发后,共有![]() 个 人参与了本次活动.
个 人参与了本次活动.
(1)x的值是多少?
(2)再经过几轮转发后,参与人数会超过![]() 人?
人?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】王老师给学生出了一道题:
求(2a+b)(2a﹣b)+2(2a﹣b)2+(2ab2﹣16a2b)÷(﹣2a)的值,其中a=![]() ,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”
,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”
(1)你认为他们谁说的有道理?为什么?
(2)若xm等于本題计算的结果,试求x2m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
如:P(1,4)的“2属派生点为P′(1+2×4,2×1+4),即P′(9,6);
(1)点P(-1,3)的“2属派生点”P′的坐标为______;
(2)若点P的“3属派生点”P′的坐标为(-1,3),则点P的坐标为______.
(3)若点P在x轴的正半轴上,点P的“k属派生点”为点P′,线段PP′的长度等于线段OP的长度,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD。过点D作DE⊥AB于E,交AC于点P,求证:点P平分线段DE。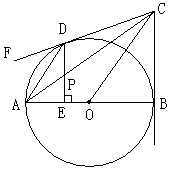
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9
(1)求证:△COD∽△CBE;
(2)求半圆O的半径 ![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
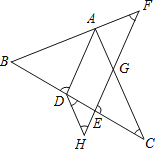
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,若∠F=40°,求∠H的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 ![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵![]() 两次共花费940元
两次共花费940元![]() 两次购进的A、B两种花草价格均分别相同
两次购进的A、B两种花草价格均分别相同![]() .
.
![]() 、B两种花草每棵的价格分别是多少元?
、B两种花草每棵的价格分别是多少元?
![]() 若再次购买A、B两种花草共12棵
若再次购买A、B两种花草共12棵![]() 、B两种花草价格不变
、B两种花草价格不变![]() ,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com