
【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 ![]() 的值
的值
【答案】
(1)
证明:∵△ABC是等腰直角三角形,
∴∠C=∠ABC=45°,
∴∠PEA=∠ABC=45°
又∵PE是⊙O的直径,
∴∠PAE=90°,
∴∠PEA=∠APE=45°,
∴ △APE是等腰直角三角形.
(2)
解:∵△ABC是等腰直角三角形,
∴AC=AB,
同理AP=AE,
又∵∠CAB=∠PAE=90°,
∴∠CAP=∠BAE,
∴△CPA≌△BAE,
∴CP=BE,
在Rt△BPE中,∠PBE=90°,PE=2,
∴PB2+BE2=PE2,
∴CP2+PB2=PE2=4.
【解析】(1)根据等腰直角三角形性质得出∠C=∠ABC=∠PEA=45°,再由PE是⊙O的直径,得出∠PAE=90°,∠PEA=∠APE=45°,从而得证.
(2)根据题意可知,AC=AB,AP=AE,再证△CPA≌△BAE,得出CP=BE,依勾股定理即可得证.


科目:初中数学 来源: 题型:
【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
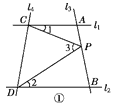
【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
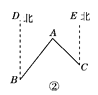
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
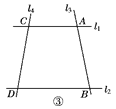
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧与墙MN平行且距离为0.8米,已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由。(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)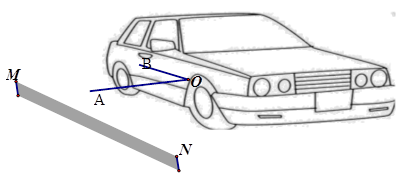
查看答案和解析>>
科目:初中数学 来源: 题型:
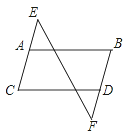
【题目】如图,有以下3句话:①AB∥CD,②∠B=∠C、③∠E=∠F、请以其中2句话为条件,第三句话为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程 ![]() ,操作步骤是:
,操作步骤是:
第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C 的横坐标m即为该方程的一个实数根(如图1)
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D 的横坐标为n即为该方程的另一个实数根。

(1)在图2 中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹)
(2)结合图1,请证明“第三步”操作得到的m就是方程 ![]() 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程 ![]() 的实数根,请你直接写出一对固定点的坐标;
的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与a,b,c之间满足怎样的关系时,点P(
与a,b,c之间满足怎样的关系时,点P( ![]() ,
, ![]() ),Q(
),Q( ![]() ,
, ![]() )就是符合要求的一对固定点?
)就是符合要求的一对固定点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下两幅统计图.请根据相关信息,解答下列问题: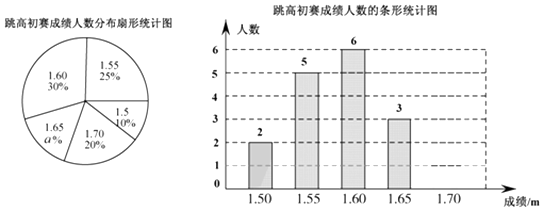
(1)扇形统计图中a= , 初赛成绩为1.70m所在扇形图形的圆心角为°;
(2)补全条形统计图;
(3)这组初赛成绩的众数是 m,中位数是 m;
(4)根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.60m的运动员杨强能否进入复赛?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB的延长线上,AC=![]() BC,D在AB的反向延长线上,BD=
BC,D在AB的反向延长线上,BD=![]() DC.
DC.
(1)在图上画出点C和点D的位置;
(2)设线段AB长为x,则BC=__ __,AD=__ __;(用含x的代数式表示)
(3)设AB=12 cm,求线段CD的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
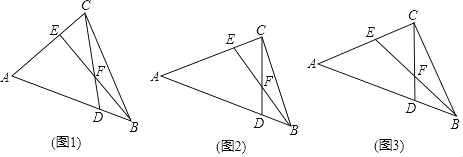
【题目】如图,在△ABC中,点D在边AB上,点E在边AC上,CE=BD,连接CD,BE,BE与CD相交于点F.
(1)如图1,若△ACD为等边三角形,且CE=DF,求∠CEF的度数;
(2)如图2,若AC=AD,求证:EF=FB;
(3)如图3,在(2)的条件下,若∠CFE=45°,△BCD的面积为4,求线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com