
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下两幅统计图.请根据相关信息,解答下列问题: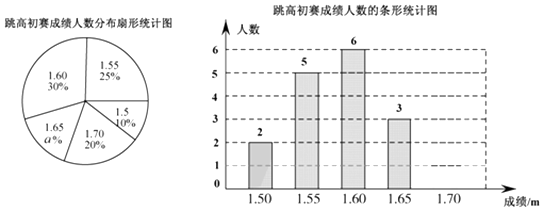
(1)扇形统计图中a= , 初赛成绩为1.70m所在扇形图形的圆心角为°;
(2)补全条形统计图;
(3)这组初赛成绩的众数是 m,中位数是 m;
(4)根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.60m的运动员杨强能否进入复赛?为什么?
【答案】
(1)15;72
(2)
解:跳170m的人数是: ![]() ×20%=4(人),
×20%=4(人),
补图如下:
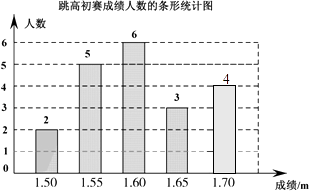
(3)1.60;1.60
(4)
解:不一定,理由如下:因为由高到低的初赛成绩中有4人是1.70m,有3人是1.65m,第8人的成绩为1.60m,但是成绩为1.60m的有6人,所以杨强不一定进入复赛.
【解析】(1.)解:根据题意得:
1﹣20%﹣10%﹣25%﹣30%=15%;
则a的值是15;
初赛成绩为1.70m所在扇形图形的圆心角为:360°×20%=72°;
所以答案是:15,72°;
(3.)解:∵在这组数据中,1.60m出现了6次,出现的次数最多,
∴这组数据的众数是1.60m;
将这组数据从小到大排列,其中处于中间的两个数都是1.60m,
则这组数据的中位数是1.60m.所以答案是:1.60,1.60;
【考点精析】根据题目的已知条件,利用扇形统计图和条形统计图的相关知识可以得到问题的答案,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】我国三国时期数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ//AB,则正方形EFGH的边长为.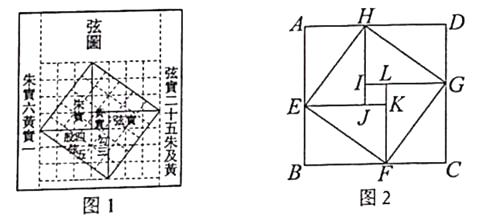
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 ![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水龙头关闭不紧会造成滴水,小明用可以显示水量的容器做图①所示的试验,并根据试验数据绘制出图②所示的容器内盛水量W(L)与滴水时间t(h)的函数关系图象,请结合图象解答下列问题:
(1)容器内原有水多少?
(2)求W与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?

图 ① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
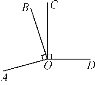
【题目】(1)如图,已知∠AOB=∠COD=90°,试写出两个与图①中角(直角除外)有关的结论:
(ⅰ)∠__ __=∠__ __,
(ⅱ)∠__ __+∠__ __=180°;
(2)请选择(1)中的一个结论说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC 中,∠A=90°,AB=AC,点 D 为 BC 的中点.
(1)点 E、F 分别为 AB、AC 上的中点,请按要求作出满足条件的△ABC 图形并证明:DE=DF;
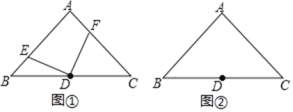
(2)如图①,若点 E、F 分别为 AB、AC 上的点,且 DE⊥DF,求证:BE=AF;
(3)若点 E、F 分别为 AB、CA 延长线上的点,且 DE⊥DF,那么 BE=AF 吗?请利用图②说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为8cm,FG是等腰直角△EFG的斜边,FG=10cm,点B、F、C、G都在直线l上,△EFG以1cm/s的速度沿直线l向右做匀速运动,当t=0时,点G与B重合,记t(0≤t≤8)秒时,正方形与三角形重合部分的面积是Scm2 , 则S与t之间的函数关系图象大致为( )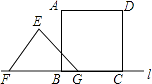
A.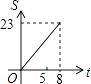
B.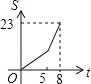
C.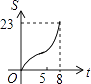
D.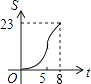
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com