
【题目】如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O,若∠BAC等于82°,则∠OBC=°. 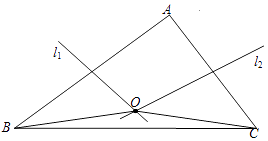
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y= ![]() (k≠0)的图象恰好经过点A′,B,则k的值为 .
(k≠0)的图象恰好经过点A′,B,则k的值为 . 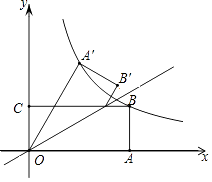
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题12分)如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3, ![]() ),B(9,5
),B(9,5 ![]() ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,
),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3, ![]() ,
, ![]() (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.

(1)求AB所在直线的函数表达式.
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.
(3)在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
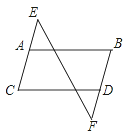
【题目】如图,有以下3句话:①AB∥CD,②∠B=∠C、③∠E=∠F、请以其中2句话为条件,第三句话为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋中有除颜色外其他完全相同的3个球,每次从袋中摸出一个球,记下颜色后放回搅匀再摸,在摸球试验中得到下表中部分数据:
摸球 总次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
摸到黄球的次数 | 14 | 23 | 38 | 52 | 67 | 86 | 97 | 111 | 120 | 136 |
摸到黄球的频率 | 35% | 32% | 33% | 35% | 35% |
(1)请将上表补充完整(结果精确到1%);
(2)制作折线统计图表示摸到黄球的频率的变化情况;
(3)估计从袋中摸出一个球是黄球的概率是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下两幅统计图.请根据相关信息,解答下列问题: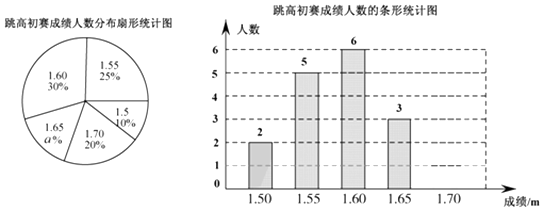
(1)扇形统计图中a= , 初赛成绩为1.70m所在扇形图形的圆心角为°;
(2)补全条形统计图;
(3)这组初赛成绩的众数是 m,中位数是 m;
(4)根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.60m的运动员杨强能否进入复赛?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
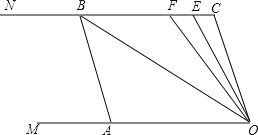
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题时需要思考:是否解决过与其类似的问题.小明从问题1解题思路中获得启发从而解决了问题2.
(1)问题1:如图①,在正方形ABCD中,E、F是BC、CD上两点,∠EAF=45°. 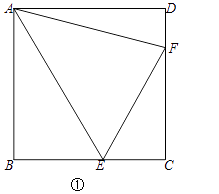
求证:∠AEF=∠AEB.
小明给出的思路为:延长EB到H,满足BH=DF,连接AH.请完善小明的证明过程.
(2)问题2:如图②,在等腰直角△ABC中,∠ACB=90°,AC=BC=4,D为AB中点,E、F是AC、BC边上两点,∠EDF=45°. 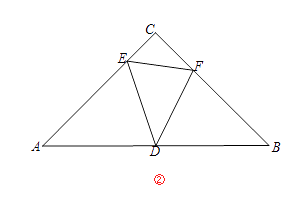
①求点D到EF的距离.
②若AE=a,则S△DEF=(用含字母a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:同弧或等弧所对的圆周角相等.也就是,如图(1),⊙O中, ![]() 所对的圆周角∠ACB=∠ADB=∠AEB.
所对的圆周角∠ACB=∠ADB=∠AEB. 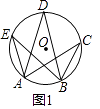
(1)已知:如图(2),矩形ABCD. 
①若AB< ![]() BC,在边AD上求作点P,使∠BPC=90°.(保留作图痕迹,写出作法.)
BC,在边AD上求作点P,使∠BPC=90°.(保留作图痕迹,写出作法.)
②小明经研究发现,当AB、BC的大小关系发生变化时,①中点P的个数也会发生变化,请你就点P的个数,探讨AB与BC之间的数量关系.(直接写出结论)
创新
(2)小明经进一步研究发现:命题“若四边形的一组对边相等和一组对角相等,则这个四边形是平行四边形.”是一个假命题,并在平行四边形的基础上利用“同弧或等弧所对的圆周角相等.”作出了一个反例图形.请你利用下面如图(3)所给的□ABCD作出该反例图形.(不写作法,保留作图痕迹) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com