
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y= ![]() (k≠0)的图象恰好经过点A′,B,则k的值为 .
(k≠0)的图象恰好经过点A′,B,则k的值为 . 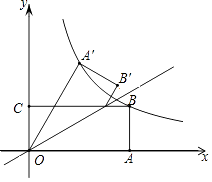
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图信息,L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象,问

(1)在刚出发时我公安快艇距走私船多少海里?
(2)计算走私船与公安快艇的速度分别是多少?
(3)写出L1,L2的解析式
(4)问6分钟时两艇相距几海里.
(5)猜想,公安快艇能否追上走私船,若能追上,那么在几分钟追上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AD 是ABC 中 BC 边上的中线,若 AB 3 , AD 4 ,则 AC 的取值范围是( )
A. 1 AC 7 B. 0.5 AC 3.5 C. 5 AC 11 D. 2.5 AC 5.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个粒子在第一象限内及x轴、y轴上运动,在第一分钟,它从原点运动到点(1,0),第二分钟,它从点(1,0)运动到点(1,1),而后它接着按图中箭头所示在与x轴,y轴平行的方向上来回运动,且每分钟移动1个单位长度,那么在第2019分钟时,这个粒子所在位置的坐标是( )
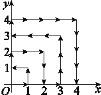
A. (44,5) B. (5,44) C. (44,6) D. (6,44)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=-x+m分别交于x轴、y轴于A,B两点,已知点C(2,0).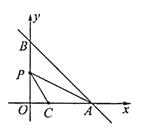
(1)当直线AB经过点C时,点O到直线AB的距离是;
(2)设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(2,2),B(4,1),C(4,4).
(1)作出 ![]() ABC关于原点O成中心对称的
ABC关于原点O成中心对称的 ![]() A1B1C1.
A1B1C1.
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 ![]() A1B1C1的内部(不包括顶点和边界),求a的取值范围.
A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
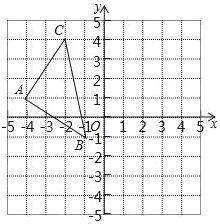
【题目】已知,△ABC在平面直角坐标系中的位置如图所示.
(1)把△ABC向下平移2个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A1B1C1关于y轴对称的△A2B2C2,并写出A2的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
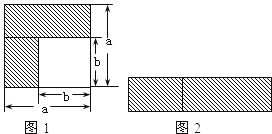
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com