
【题目】已知,在△ABC 中,∠A=90°,AB=AC,点 D 为 BC 的中点.
(1)点 E、F 分别为 AB、AC 上的中点,请按要求作出满足条件的△ABC 图形并证明:DE=DF;
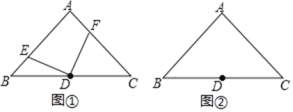
(2)如图①,若点 E、F 分别为 AB、AC 上的点,且 DE⊥DF,求证:BE=AF;
(3)若点 E、F 分别为 AB、CA 延长线上的点,且 DE⊥DF,那么 BE=AF 吗?请利用图②说明理由.
【答案】(1)见解析;(2)见解析;(3) BE=AF,见解析.
【解析】
(1)画图并证明△AED≌△AFD,可得DE=DF;
(2)如图①,证明△BDE≌△ADF,可得BE=AF;
(3)如图②,证明△EDB≌△FDA,可得BE=AF.
(1)如图,连接AD.

∵∠A=90°,AB=AC,点D为BC的中点,∴∠EAD=∠FAD.
∵点E、F分别为AB、AC上的中点,∴AE![]() AB,AF
AB,AF![]() AC.
AC.
在△AED和△AFD中,∵ ,∴△AED≌△AFD(SAS),∴DE=DF;
,∴△AED≌△AFD(SAS),∴DE=DF;
(2)连接AD,如图①所示.
∵∠BAC=90°,AB=AC,∴△ABC为等腰直角三角形,∠B=45°.
∵点D为BC的中点,∴AD![]() BC=BD,∠FAD=45°.
BC=BD,∠FAD=45°.
∵∠BDE+∠EDA=90°,∠EDA+∠ADF=90°,∴∠BDE=∠ADF.
在△BDE和△ADF中,∵ ,∴△BDE≌△ADF(ASA),∴BE=AF;
,∴△BDE≌△ADF(ASA),∴BE=AF;
(3)BE=AF.证明如下:
连接AD,如图②所示.
∵∠ABD=∠BAD=45°,∴∠EBD=∠FAD=135°.
∵∠EDB+∠BDF=90°,∠BDF+∠FDA=90°,∴∠EDB=∠FDA.
在△EDB和△FDA中,∵ ,∴△EDB≌△FDA(ASA),∴BE=AF.
,∴△EDB≌△FDA(ASA),∴BE=AF.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
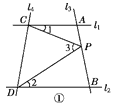
【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
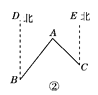
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
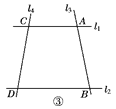
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下两幅统计图.请根据相关信息,解答下列问题: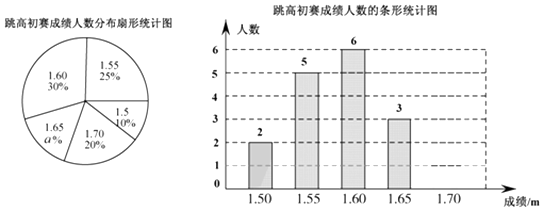
(1)扇形统计图中a= , 初赛成绩为1.70m所在扇形图形的圆心角为°;
(2)补全条形统计图;
(3)这组初赛成绩的众数是 m,中位数是 m;
(4)根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.60m的运动员杨强能否进入复赛?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB的延长线上,AC=![]() BC,D在AB的反向延长线上,BD=
BC,D在AB的反向延长线上,BD=![]() DC.
DC.
(1)在图上画出点C和点D的位置;
(2)设线段AB长为x,则BC=__ __,AD=__ __;(用含x的代数式表示)
(3)设AB=12 cm,求线段CD的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题时需要思考:是否解决过与其类似的问题.小明从问题1解题思路中获得启发从而解决了问题2.
(1)问题1:如图①,在正方形ABCD中,E、F是BC、CD上两点,∠EAF=45°. 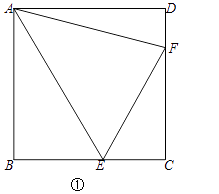
求证:∠AEF=∠AEB.
小明给出的思路为:延长EB到H,满足BH=DF,连接AH.请完善小明的证明过程.
(2)问题2:如图②,在等腰直角△ABC中,∠ACB=90°,AC=BC=4,D为AB中点,E、F是AC、BC边上两点,∠EDF=45°. 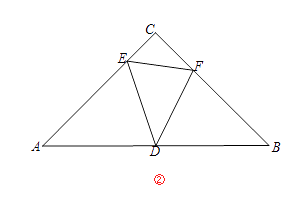
①求点D到EF的距离.
②若AE=a,则S△DEF=(用含字母a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2条直线 最多有![]() =1个交点,3条直线最多有
=1个交点,3条直线最多有![]() =3个交点,4条直线最多有
=3个交点,4条直线最多有![]() =6个交点,……由此猜想,8条直线最多有___个交点.
=6个交点,……由此猜想,8条直线最多有___个交点.

A. 32 B. 16 C. 28 D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计。图(1)与图(2)是整理数据后绘制的两幅不完整的统计图。以下结论不正确的是( )
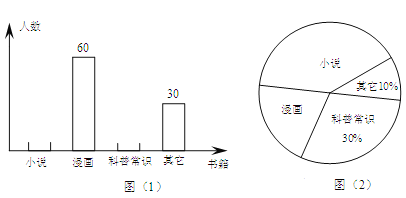
A. 由这两个统计图可知喜欢“科普常识”的学生有90人.
B. 若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360个.
C. 由这两个统计图不能确定喜欢“小说”的人数.
D. 在扇形统计图中,“漫画”所在扇形的圆心角为72°.
查看答案和解析>>
科目:初中数学 来源: 题型:
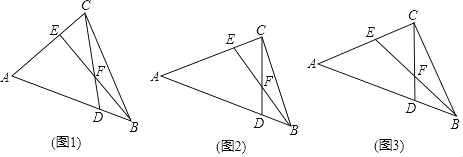
【题目】如图,在△ABC中,点D在边AB上,点E在边AC上,CE=BD,连接CD,BE,BE与CD相交于点F.
(1)如图1,若△ACD为等边三角形,且CE=DF,求∠CEF的度数;
(2)如图2,若AC=AD,求证:EF=FB;
(3)如图3,在(2)的条件下,若∠CFE=45°,△BCD的面积为4,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.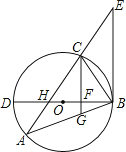
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG= ![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com