
【题目】如图,已知AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD。过点D作DE⊥AB于E,交AC于点P,求证:点P平分线段DE。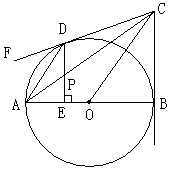
【答案】证明:连结OD , OD∥AD , 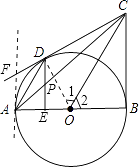
∴∠1=∠ADO , ∠2=∠DAO ,
∵OA=OD , ∴∠ADO=∠DAO ,
∴∠1=∠2,∵OD=OB,OC=OC,
∴△ODC≌△OBC , ∴∠ODC=∠OBC。
∵OB是⊙O的半径,BC是⊙O的切线,
∴BC⊥OB
∴∠OBC=900 , ∴∠ODC=900 , ∴CD⊥OD。
∴CD是⊙O的切线。
过A作⊙O的切线AF , 交CD的延长线于点F , 则FA⊥AB。
∵DE⊥AB , CB⊥AB , ∴FA∥DE∥CB,
∴ ![]() 。
。
在△FAC中,∵DP∥FA, ∴ ![]() 。
。
∵FA、FD是⊙O的切线,∴FA=FD,∴ ![]() 。
。
在△ABC中,∵EP∥BC, ∴ ![]() 。
。
∵CD、CB是⊙O的切线,∴CB=CD , ![]() ,
,
∴ ![]() , ∴DP=EP ,
, ∴DP=EP ,
∴点P平分线段DE.
【解析】出现切线时,连接圆心和切点,过A作平行线,可由DP∥FA得到 ![]() ,可由EP∥BC得到
,可由EP∥BC得到![]() ,再利用切线长定理得出CB=CD,进而证出DP=EP.
,再利用切线长定理得出CB=CD,进而证出DP=EP.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,点E在CD上,连接AE,BD,点G是AE中点,过点G作FH⊥AE,FH分别交AD,BC于点F,H,FH与BD交于点K,且HK=2FG,若EG=![]() ,则线段AF的长为_______________.
,则线段AF的长为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则S△DAC:S△ABC=_____.
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则S△DAC:S△ABC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请![]() 个好友转发,每个好友转发之后,又邀请
个好友转发,每个好友转发之后,又邀请![]() 个互不相同的好友转发,已知经过两轮转发后,共有
个互不相同的好友转发,已知经过两轮转发后,共有![]() 个 人参与了本次活动.
个 人参与了本次活动.
(1)x的值是多少?
(2)再经过几轮转发后,参与人数会超过![]() 人?
人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格规定如下表:
我校初二(1),(2)两个班共104人准备利用假期去游览该景点,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人,经估算,如果两班都以班为单位分别购票,则一共应付1240元,问两班各有多少名学生? 你认为还有没有好的方法去节省门票的费用?若有,请按照你的方法计算一下能省多少钱?(
购票人数 | 1-50人 | 51-100人 | 100人以上 |
每人门票价 | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D. 
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com