
【题目】设m是整数,关于x的方程mx2-(m-1)x+1=0有有理根,则方程的根为( )。
A.![]()
B.![]() x=-1
x=-1
C.![]()
D.有无数个根
【答案】C
【解析】(1)当m=0,原方程变为:x+1=0,
解得x=-1,为有理根;(2)当m≠0,原方程为一元二次方程,
∵方程mx2-(m-1)x+1=0有有理根,
∴△=b2-4ac为完全平方数,即△=(m-1)2-4m=(m-3)2-8为完全平方数,
而m是整数,
∴设(m-3)2-8=n2 , 即(m-3)2=8+n2 ,
∴完全平方数的末位数只能为1,4,5,6,9.
∴n2的末位数只能为1,6,而大于10的两个完全平方数相差大于8,
∴n=1,
∴m-3=3,即m=6,
所以方程为:6x2-5x+1=0,(2x-1)(3x-1)=0,
∴x1= ![]() ,x2=
,x2= ![]() ,
,
答案为:C.
可分为m=0与m![]() 0两类,当方程为一元二次方程时,有理根可从判别式为完全平方数入手,进而求出m的值,再求出根.
0两类,当方程为一元二次方程时,有理根可从判别式为完全平方数入手,进而求出m的值,再求出根.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,△ABC中,∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F;
①若∠B=90°则∠F= ;
②若∠B=a,求∠F的度数(用a表示);
(2)如图2所示,若点G是CB延长线上任意一动点,连接AG,∠AGB与∠GAB的角平分线交于点H,随着点G的运动,∠F+∠H的值是否变化?若变化,请说明理由;若不变,请求出其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°, AB//CD,M为BC边上的一点,AM平分∠BAD,DM平分∠ADC,
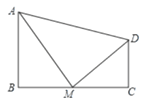
求证:(1) AM⊥DM;
(2) M为BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD。过点D作DE⊥AB于E,交AC于点P,求证:点P平分线段DE。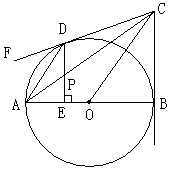
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,对角线AC、BD交于点O,且分别平分∠DAB,∠ABC.
中,对角线AC、BD交于点O,且分别平分∠DAB,∠ABC.
(1)请求出∠AOB的度数,写出AD、AB、BC之间的等量关系,并给予证明.
(2)设点P为对角线AC上一点,PB=5,若AD+BC=16,四边形ABCD的面积为![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )

A. ﹣2<m<![]() B. ﹣3<m<﹣
B. ﹣3<m<﹣![]() C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com