
【题目】已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由.
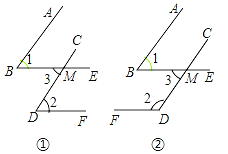
(1)如图①,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(2)如图②,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(3)经过上述证明,我们可得出结论,如果一个角的两边与另一个角的两边分别平行,那么这两个角 ;
(4)若这两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
【答案】(1)∠1=∠2,证明详见解析;(2)∠1+∠2=180°,理由详见解析;(3)相等或互补;(4)30°,30°或60°,120°.
【解析】
1)由AB∥CD可得∠1=∠3,由BE∥DF可得∠3=∠2,即可得到结果;
(2)由AB∥CD可得∠1=∠3,由BE∥DF可得∠3+∠2=180°,即可得到结果;
(3)结合(1)(2)中得出的结论即可作出判断.
(4)根据题示判断出两角互补或相等,列出方程求解即可.
解:(1)∠1=∠2.
证明如下:∵AB∥CD,
∴∠1=∠3,
∵BE∥DF,
∴∠2=∠3,
∴∠1=∠2;
(2)∠1+∠2=180°.
理由:∵AB∥CD,
∴∠1=∠3,
∵BE∥DF,
∴∠2+∠3=180°,
∴∠1+∠2=180°;
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补;
(4)设一个角的度数为x,则另一个角的度数为3x-60°,
当x=3x-60°,解得x=30°,则这两个角的度数分别为30°,30°;
当x+3x-60°=180°,解得x=60°,则这两个角的度数分别为60°,120°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为 . 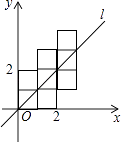
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣ ![]() ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2 ![]() ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2 ![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
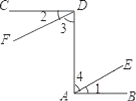
【题目】已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.
某同学在解决上面问题时,准备三步走,请你完成他的步骤.
(1)问题的结论:DF____AE.
(2)思路要使DF_____AE,只要∠3=____.
(3)说理过程:
解:∵CD⊥DA,DA⊥AB,
∴∠CDA=∠DAB=________.( )
又∵∠1=∠2,
∴∠CDA﹣∠2=____﹣____,( )
即∠3=______,
∴DF_____AE.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线m经过A(4,0)、B(3,﹣![]() ),直线n经过原点且与直线m相交于D,D点的横坐标为﹣2.
),直线n经过原点且与直线m相交于D,D点的横坐标为﹣2.
(1)求直线m、n的表达式;
(2)求△OBD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( ) 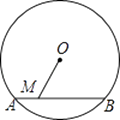
A.3≤OM≤5
B.4≤OM≤5
C.3<OM<5
D.4<OM<5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com