
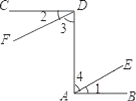
����Ŀ����֪����ͼ��CD��DA��DA��AB����1=��2����ȷ������DF��AE��λ�ù�ϵ����˵��������ɣ�
ijͬѧ�ڽ����������ʱ���������ߣ�����������IJ��裮
(1)����Ľ��ۣ�DF____AE��
(2)˼·ҪʹDF_____AE��ֻҪ��3=____��
(3)˵�����̣�
�⣺��CD��DA��DA��AB��
���CDA=��DAB=________��( )
�֡ߡ�1=��2��
���CDA����2=____��____��( )
����3=______��
��DF_____AE��( )
���𰸡��Σ��Σ���4��90������ֱ���壬��DAB����1����ʽ�����ʣ���4���Σ��ڴ�����ȣ���ֱ��ƽ�У�
��������
������֪�������Լ�ƽ���ߵ��ж�������ռ��ɣ�
�⣺��1������Ľ��ۣ�DF��AE��
��2��˼·ҪʹDF��AE��ֻҪ��3=��4��
��3��˵�����̣�
�⣺��CD��DA��DA��AB��
���CDA=��DAB=90������ ��ֱ���壩
�֡ߡ�1=��2��
���CDA-��2=��BAD-��1���� ��ʽ�����ʣ�
����3=��4��
��DF��AE���� �ڴ�����ȣ���ֱ��ƽ�У���
�ʴ�Ϊ���Σ��Σ���4��90������ֱ���壬��DAB����1����ʽ�����ʣ���4���Σ��ڴ�����ȣ���ֱ��ƽ�У�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90�㣬BC�Ĵ�ֱƽ����EF��BC�ڵ�D����AB�ڵ�E����BE=BF������һ���������Բ���֤���ı���BECFΪ�����ε���

A. BC=AC B. CF��BF C. BD=DF D. AC=BF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
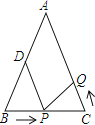
����Ŀ����ͼ��ʾ����֪��ABC�У�AB��AC��10cm��BC��8cm����DΪAB���е㣮�����P���߶�BC����B������C���˶���ͬʱ��Q���߶�CA����C�������A���˶������˶�ʱ��Ϊt�룮
��1������P���ٶ�Ϊ3cm/s���ú�t��ʽ�ӱ�ʾ��t��ʱ��BP���� ��cm��CP���� ��cm��
��2���ڣ�1���������£�����Q�˶��ٶ����P���˶��ٶ���ȣ�������������BPD����CQPȫ�ȣ�˵�����ɣ�
��3������Q���˶��ٶ����P���˶��ٶȲ���ȣ��ҵ�P���ٶȱȵ�Q���ٶ���1cm/sʱ����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD����CQPȫ�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬С��һ�ҳ�������ǰ��ij�����Σ��ƻ��ڶ�����������Դ�����Լݳ��Ρ�
����������Ϣ������������⣺
��1�����ʱ��Ϊ ![]() Сʱ�����ü�˾�ij��������Ϊ
Сʱ�����ü�˾�ij��������Ϊ ![]() Ԫ�������ҹ�˾�ij��������Ϊ
Ԫ�������ҹ�˾�ij��������Ϊ ![]() Ԫ���ֱ����
Ԫ���ֱ���� ![]() ��
�� ![]() ����
���� ![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2���������С�����㲢ѡ���ĸ����η������㡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���֪һ�κ���
�У���֪һ�κ���![]() ��ͼ����
��ͼ����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ����
����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ��
��

��1�����![]() ����͵�
����͵�![]() ���ꣻ
���ꣻ
��2����![]() ���߶�
���߶�![]() ��һ�㣬��
��һ�㣬��![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() �ڵڶ����ޣ����ı���
�ڵڶ����ޣ����ı���![]() Ϊ���Σ����
Ϊ���Σ����![]() ���ꣻ
���ꣻ
��3���ڣ�2���������£���![]() Ϊƽ��ֱ������ϵ��һ�㣬��
Ϊƽ��ֱ������ϵ��һ�㣬��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı�����ƽ���ı��Σ���ֱ��д����������������
Ϊ������ı�����ƽ���ı��Σ���ֱ��д����������������![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
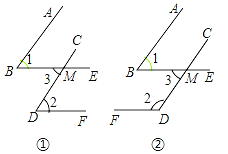
����Ŀ����֪һ���ǵ���������һ���ǵ����߷ֱ�ƽ�У�����ͼ��̽����������֮��Ĺ�ϵ����˵�����ɣ�
��1����ͼ�٣�AB��CD��BE��DF����1���2�Ĺ�ϵ�� ��
֤����
��2����ͼ�ڣ�AB��CD��BE��DF����1���2�Ĺ�ϵ�� ��
֤����
��3����������֤�������ǿɵó����ۣ����һ���ǵ���������һ���ǵ����߷ֱ�ƽ�У���ô�������� ��
��4�����������ǵ����߷ֱ�ƽ�У���һ���DZ���һ���ǵ�3����60�㣬���������Ƿֱ��Ƕ��ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
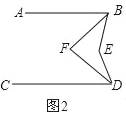
����Ŀ����֪��ֱ��AB��CD
��1����ͼ1����E��ֱ��BD����࣬�����ABE����CDE����BED��������ϵ����֤����Ľ��ۣ�
��2����ͼ2����E��ֱ��BD����࣬BF��DF�ֱ�ƽ�֡�ABE����CDE�������BFD�͡�BED��������ϵ����֤����Ľ��ۣ�
��3����ͼ3����E��ֱ��BD���Ҳ࣬BF��DF�ֱ�ƽ�֡�ABE����CDE����ô�ڣ�2�����С�BFD�͡�BED��������ϵ�IJ����Ƿ��Գ����������������֤�����������������д����IJ��룬��֤����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC��ֱ�Ƕ���A��ʱ����ת90��õ���ADE��BC���ӳ��߽�DE��F������BD����BC��2EF����֤����BED�ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������̣�

��ͼ����֪��1 ����2����B ����C�����Ƶ�AB��CD���������£�
�ߡ�1 ����2����֪����
����1 ����CGD��______________ _________����
���2 ����CGD��������������
��CE��BF��___________________ ________����
��� ����C��__________________________����
���ߡ�B ����C����֪����
��� ����B��������������
��AB��CD��________________________________����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com