
【题目】如图,在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() 的图像与
的图像与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.

(1)求点![]() 坐标和点
坐标和点![]() 坐标;
坐标;
(2)点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 为坐标原点,点
为坐标原点,点![]() 在第二象限,且四边形
在第二象限,且四边形![]() 为菱形,求点
为菱形,求点![]() 坐标;
坐标;
(3)在(2)的条件下,点![]() 为平面直角坐标系中一点,以
为平面直角坐标系中一点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,请直接写出所有满足条件的
为顶点的四边形是平行四边形,请直接写出所有满足条件的![]() 点坐标.
点坐标.
【答案】(1)![]() ,
,![]() ;(2)D
;(2)D![]() ;(3)
;(3)![]() ;
;![]() ;
;![]()
【解析】
(1)分别令x与y为0,求出对应y与x的值,即可确定出A与B的坐标;
(2)设点![]() 坐标为
坐标为![]() ,根据题意知
,根据题意知![]() ,根据两点之间的距离公式即可求得点
,根据两点之间的距离公式即可求得点![]() 的坐标,利用轴对称的性质即可求得点
的坐标,利用轴对称的性质即可求得点![]() 的坐标;
的坐标;
(3)过A作BD的平行线![]() ,过D作AB的平行线
,过D作AB的平行线![]() ,过B作AD的平行线
,过B作AD的平行线![]() ,分别相交于
,分别相交于![]() 、
、![]() 、
、![]() ,利用待定系数法分别求得直线
,利用待定系数法分别求得直线![]() 、
、![]() 、
、![]() 的解析式,再求直线的交点坐标即可求解.
的解析式,再求直线的交点坐标即可求解.
(1)当![]() 时,得
时,得![]() ,解得:
,解得:![]()
∴点B的坐标为(0,4),
当![]() 时,得
时,得![]() ,解得:
,解得:![]()
∴点A的坐标为(2,0);
(2)∵点![]() 是线段
是线段![]() 上,
上,
∴设点![]() 坐标为
坐标为![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,
则![]() ,
,
解得![]() .
.
∴点![]() 坐标为
坐标为![]() .
.
∵点![]() 、
、![]() 关于
关于![]() 轴对称,
轴对称,
∴点![]() 坐标为
坐标为![]() ;
;
(3)过A作BD的平行线![]() ,过D作AB的平行线
,过D作AB的平行线![]() ,过B作AD的平行线
,过B作AD的平行线![]() ,分别相交于
,分别相交于![]() 、
、![]() 、
、![]() ,如图:
,如图:

∵点A、B、D的坐标分别为(2,0),(0,4),(-1,2),
设BD的解析式为![]() ,
,
把点D的坐标 (-1,2)代入得:![]() ,
,
解得:![]() ,
,
∴设直线![]() 的解析式为
的解析式为![]() ,
,
把点A的坐标 (2,0)代入得:![]() ,
,
解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
同理可求得直线![]() 、
、![]() 的解析式分别为
的解析式分别为![]() 、
、![]() ,
,
联立![]() 、
、![]() 得:
得:![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为(1,-2);
的坐标为(1,-2);
联立![]() 、
、![]() 得:
得: ,解得
,解得![]() ,
,
∴点![]() 的坐标为(3,2);
的坐标为(3,2);
联立![]() 、
、![]() 得:
得: ,解得
,解得![]() ,
,
∴点![]() 的坐标为(-3,6);
的坐标为(-3,6);
综上,所有满足条件的![]() 点坐标为(1,-2),(3,2),(-3,6);
点坐标为(1,-2),(3,2),(-3,6);


科目:初中数学 来源: 题型:
【题目】如图,已知 OACB 的顶点 O、A、B 的坐标分别是(0,a)、(b,0),且a、b 满足![]()
![]()
![]() b .
b .
(1)如图 1,a= ,b= ,点 C 的坐标 .
(2)如图 2,点 P 为边 OB 上一动点,将线段 AP 绕 P 点顺时针旋转 90°至 PD.当点 P 从O 运动到 B 的过程中,求点 D 运动路径的长度.
(3)如图 3,在(2)的条件下,作等腰 Rt△BED,且∠DBE=90°,再作等腰 Rt△ECF, 且∠ECF=90°,直线 FE 分别交 AC、OB 于点 M、N,求证:FM=EN.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
A.1.4
B.1.1
C.0.8
D.0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.
某同学在解决上面问题时,准备三步走,请你完成他的步骤.
(1)问题的结论:DF____AE.
(2)思路要使DF_____AE,只要∠3=____.
(3)说理过程:
解:∵CD⊥DA,DA⊥AB,
∴∠CDA=∠DAB=________.( )
又∵∠1=∠2,
∴∠CDA﹣∠2=____﹣____,( )
即∠3=______,
∴DF_____AE.( )
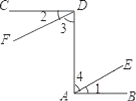
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE中.
(1)AC与BE相交于P,求证:四边形PEDC为菱形;
(2)延长DC、AE交于M点,连BM交CE于N,求证:CN=EP;
(3)若正五边形边长为2,直接写出AD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求证:∠AEB=∠ACF;
(2)求证:EF2BF22AC2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com