
【题目】如图,已知 OACB 的顶点 O、A、B 的坐标分别是(0,a)、(b,0),且a、b 满足![]()
![]()
![]() b .
b .
(1)如图 1,a= ,b= ,点 C 的坐标 .
(2)如图 2,点 P 为边 OB 上一动点,将线段 AP 绕 P 点顺时针旋转 90°至 PD.当点 P 从O 运动到 B 的过程中,求点 D 运动路径的长度.
(3)如图 3,在(2)的条件下,作等腰 Rt△BED,且∠DBE=90°,再作等腰 Rt△ECF, 且∠ECF=90°,直线 FE 分别交 AC、OB 于点 M、N,求证:FM=EN.



【答案】(1)![]() ;
;![]() ;(
;(![]() ,
,![]() );(2)
);(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据![]()
![]()
![]() b 可得
b 可得![]() 且
且![]() ,从而确定a的值,代入求得b的值,然后利用平行四边形的性质确定点C的坐标;
,从而确定a的值,代入求得b的值,然后利用平行四边形的性质确定点C的坐标;
(2)点P的运动轨迹为一条线段,则点D的运动轨迹也为一条线段,当点P与点O重合时,点D与点B重合,当点P与点B重合时,点D的位置如图1所示,点D的运动路径为BD,然后利用正方形和旋转的性质算出BD=![]() ;
;
(3)由(2)点D的运动路径可知点D在∠OBC的外角平分线上,过点F作FG垂直AC于点G,过E作EH垂直AC于点H,已知△FCE为等腰直角三角形,可推出△FGC≌△CHE(AAS),过点E作EQ垂直OB于点Q,可推出△FGM≌△ENQ(AAS),可得FM=EN.
解:∵![]()
![]()
![]() b
b
∴![]() 且
且![]()
解得![]()
∴将![]() 代入
代入![]()
![]()
![]() b
b
∴b=![]()
∴A(0,![]() )、B(
)、B(![]() ,0)
,0)
∴OA=OB=![]() ,
,
∵四边形OACB为平行四边形,∠AOB=90°,
∴四边形OACB为正方形,
∴C点坐标为(![]() ,
,![]() )
)
故答案为:![]() ;
;![]() ;(
;(![]() ,
,![]() );
);
(2)如图1所示,
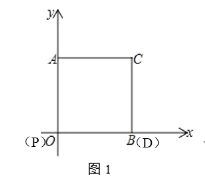
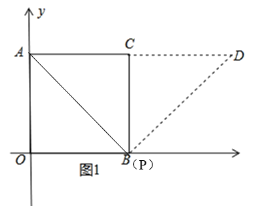
∵点P的运动轨迹为一条线段,则点D的运动轨迹也为一条线段,
当点P与点O重合时,点D与点B重合,当点P与点B重合时,点D的位置如图1所示,
∴点D的运动路径为BD,
又∵线段 AP 绕 P 点顺时针旋转 90°至 PD且由(1)可知四边形四边形OACB为正方形
∴BD=AB=![]() ;
;
(3)如图2所示,
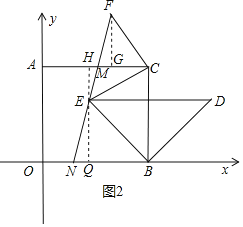
由(2)点D的运动路径可知点D在∠OBC的外角平分线上,
∴∠DBC=∠EBC=∠EBO=45°,
∴ED∥OB,
过点F作FG垂直AC于点G,过E作EH垂直AC于点H,
∴∠FGC=∠EHC=90°,
∵△FCE为等腰直角三角形,
∴FC=EC,∠FCE=90°,
∵∠ACB=90°,
∴∠FCG=∠ECB=∠CEH,
∴△FGC≌△CHE(AAS),
∴CH=FG,
过点E作EQ垂直OB于点Q,
则BQ=EQ=CH=FG,
∵∠FGM=∠EQN=90°,
∠FMG=∠ENQ,
∴△FGM≌△ENQ(AAS),
∴FM=EN.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】越来越多的人在用微信支付、转账,把微信账户里的钱转到银行卡叫做提现,自2016年3月1日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为1800元,他需支付手续费_____元;
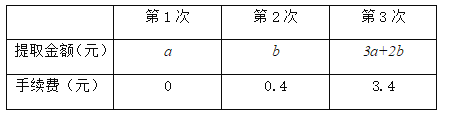
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下,问:小明3次提现金额共计多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)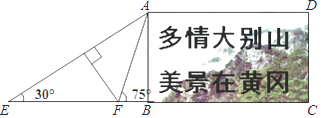
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,顺次连接长宽不等的矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边中点,得到图 3.如 此反复操作下去,则第 2021 个图形中直角三角形的个数有_____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形 ABCD 中,E 为 BC 的中点,F 是 CD 上一点,且 CF ![]() CD ,
CD ,

求证:(1)∠AEF=90°;
(2) ∠BAE=∠EAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是

A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:k取任何实数值,方程总有实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).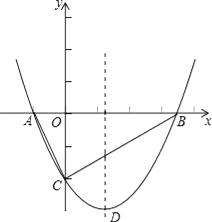
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() 的图像与
的图像与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.

(1)求点![]() 坐标和点
坐标和点![]() 坐标;
坐标;
(2)点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 为坐标原点,点
为坐标原点,点![]() 在第二象限,且四边形
在第二象限,且四边形![]() 为菱形,求点
为菱形,求点![]() 坐标;
坐标;
(3)在(2)的条件下,点![]() 为平面直角坐标系中一点,以
为平面直角坐标系中一点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,请直接写出所有满足条件的
为顶点的四边形是平行四边形,请直接写出所有满足条件的![]() 点坐标.
点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com