
【题目】已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:k取任何实数值,方程总有实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
【答案】
(1)证明:∵△=b2﹣4ac=(k+2)2﹣8k=(k﹣2)2≥0,∴无论k取任意实数值,方程总有实数根;
(2)解:把x=1代入x2-(k+2)x+2k=0中,1-(k+2)+2k=0,k=1,
把k=1代入x2-(k+2)x+2k=0中,
x=1或x=2,
所以方程的另一根是2.
①当1,2为直角边时,斜边为 ![]()
此时直角三角形周长为 ![]()
②当2为斜边,1为直角边时,另一直角边为 ![]()
此时直角三角形周长为 ![]()
综上所述,直角三角形的周长为 ![]() .
.
【解析】(1)首先算出此方程的△=b2﹣4ac=(k+2)2﹣8k=(k﹣2)2,根据平方的非负性得出≥0,从而得出结论k取任何实数值,方程总有实数根;
(2)根据方程根的定义把把x=1代入x2-(k+2)x+2k=0中 ,得出一个关于k的一元一次方程,解方程得出k的值,从而把k=1代入x2-(k+2)x+2k=0中,得出一个关于x的方程,解方程得出方程的另一个根;然后分类讨论:①当1,2为直角边时,根据勾股定理得出斜边的长,从而算出直角三角形的周长;②当2为斜边,1为直角边时,根据勾股定理算出另一直角边的长,从而算出直角三角形的周长 ;综上所述,得出结论。


科目:初中数学 来源: 题型:
【题目】如图,已知 OACB 的顶点 O、A、B 的坐标分别是(0,a)、(b,0),且a、b 满足![]()
![]()
![]() b .
b .
(1)如图 1,a= ,b= ,点 C 的坐标 .
(2)如图 2,点 P 为边 OB 上一动点,将线段 AP 绕 P 点顺时针旋转 90°至 PD.当点 P 从O 运动到 B 的过程中,求点 D 运动路径的长度.
(3)如图 3,在(2)的条件下,作等腰 Rt△BED,且∠DBE=90°,再作等腰 Rt△ECF, 且∠ECF=90°,直线 FE 分别交 AC、OB 于点 M、N,求证:FM=EN.



查看答案和解析>>
科目:初中数学 来源: 题型:
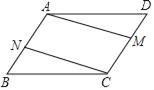
【题目】如图,在四边形ABCD中,AB∥CD,AD∥BC,AN=CM.
(1)求证:BN=DM;
(2)若BC=3,CD=2,∠B=50°,求∠BCD、∠D的度数及四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )
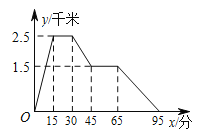
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.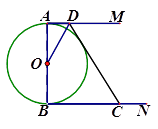
(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x > 0),BC=y (y > 0). 求y关于x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com