
【题目】已知:PA、PB、EF分别切⊙O于A、B、D,若PA=15cm,那么△PEF周长是cm.若∠P=50°,那么∠EOF= . 
【答案】30;65°
【解析】解:∵PA、PB、EF分别切⊙O于A、B、D,
∴PA=PB=15cm,ED=EA,FD=DB,
∴PE+EF+PF=PE+ED+PF+FD=PA+PB=30(cm)即△PEF周长是30cm;
∵PA、PB为⊙O的切线,
∴∠PAO=∠PBO=90°,
而∠P=50°,
∴∠AOB=360°﹣90°﹣90°﹣50°=130°;
连OD,如图,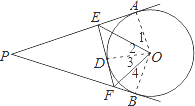
∴∠ODE=∠ODF=90°,
易证得Rt△OAE≌Rt△ODE,Rt△OFD≌Rt△OFB,
∴∠1=∠2,∠3=∠4,
∴∠2+∠3= ![]() ∠AOB=65°,则∠EOF=65°.
∠AOB=65°,则∠EOF=65°.
根据切线长定理证得ED=EA,FD=DB,再根据△PEF周长=PE+EF+PF,证得△PEF周长等于2PA。即可得出答案;连接OD,OA,OB。根据直角三角形的全等判定证得Rt△OAE≌Rt△ODE,Rt△OFD≌Rt△OFB,再根据全等三角形的性质得出∠1=∠2,∠3=∠4,就可证得∠EOF=![]() ∠AOB。再在四边形APBO中根据四边形的内角和定理求出∠AOB的度数,即可求出∠EOF的度数。
∠AOB。再在四边形APBO中根据四边形的内角和定理求出∠AOB的度数,即可求出∠EOF的度数。


科目:初中数学 来源: 题型:
【题目】如图,有A、B、C三种不同型号的卡片,每种卡片各有9张.其中A型卡片是边长为3的正方形,B型卡片是相邻两边长分别为3、1的长方形,C型卡片是边长为1的正方形.从其中取若干张卡片(每种卡片至少取1张),若把取出的这些卡片拼成一个正方形,则所拼正方形的边长的最大值是______.
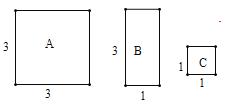
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,![]() ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
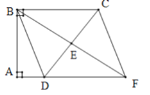
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越来越多的人在用微信支付、转账,把微信账户里的钱转到银行卡叫做提现,自2016年3月1日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为1800元,他需支付手续费_____元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下,问:小明3次提现金额共计多少元?
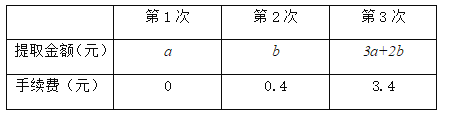
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线BC//ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(t+1,t+2),点B(t+3,t+1),将点A向右平移3个长度单位,再向下平移4个长度单位得到点C.
(1)用t表示点C的坐标为_______;用t表示点B到y轴的距离为___________;
(2)若t=1时,平移线段AB,使点A、B到坐标轴上的点![]() 、
、![]() 处,指出平移的方向和距离,并求出点
处,指出平移的方向和距离,并求出点![]() 、
、![]() 的坐标;
的坐标;
(3)若t=0时,平移线段AB至MN(点A与点M对应),使点M落在x轴的负半轴上,三角形MNB的面积为4,试求点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).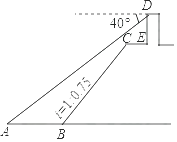
A.5.1米
B.6.3米
C.7.1米
D.9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)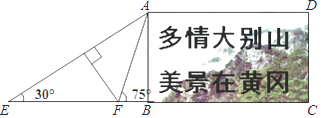
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:k取任何实数值,方程总有实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com