练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，添加一个条件，仍不能证明四边形BECF为正方形的是

    A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF

    【答案】D

    【解析】

    试题∵EF垂直平分BC，∴BE=EC，BF=CF。

    ∵CF=BE，∴BE=EC=CF=BF。∴四边形BECF是菱形。

    当BC=AC时，∠ACB=90°，∠A=45°，∴∠EBC=45°。∴∠EBF=2∠EBC=2×45°=90°。∴菱形BECF是正方形。故选项A不符合题意。

    当CF⊥BF时，利用正方形的判定得出，菱形BECF是正方形，故选项B不符合题意。

    当BD=DF时，利用正方形的判定得出，菱形BECF是正方形，故选项C不符合题意。

    当AC=BD时，无法得出菱形BECF是正方形，故选项D符合题意。

    故选D。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图①，在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE=PB．

    （1）求证：△BCP≌△DCP；

    （2）求证：∠DPE=∠ABC；

    （3）把正方形ABCD改为菱形，其它条件不变（如图②），若∠ABC=58°，则∠DPE=　 　度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知A、B两地相距10千米，上午9：00甲骑电动车从A地出发到B地，9:10乙开车从B地出发到A地，甲、乙两人距A 地距离y（千米）与甲所用的时间x(分）之间的关系如图所示。

    （1）甲的速度是 千米/分。

    （2）乙的速度是 千米/分，乙到达A地的时间是 。

    （3）甲、乙两人相距4千米的时间是 。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序按图中“→”方向排列，如（1，0）→（2，0）→（2，1）→（1，1）→（1，2）→（2，2）→，…，根据这个规律，第2019个点的坐标为______．

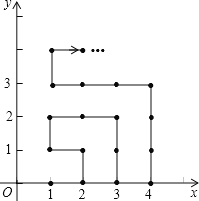
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知 OACB 的顶点 O、A、B 的坐标分别是（0，a）、（b，0），且a、b 满足 b ．

    （1）如图 1，a= ，b= ，点 C 的坐标 ．

    （2）如图 2，点 P 为边 OB 上一动点，将线段 AP 绕 P 点顺时针旋转 90°至 PD．当点 P 从O 运动到 B 的过程中，求点 D 运动路径的长度．

    （3）如图 3，在（2）的条件下，作等腰 Rt△BED，且∠DBE＝90°，再作等腰 Rt△ECF， 且∠ECF＝90°，直线 FE 分别交 AC、OB 于点 M、N，求证：FM＝EN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC 中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F

    （1）求证：EO=FO；

    （2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，图象中所反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又 去早餐店吃早餐，然后散步走回家，其中 x 表示时间，y 表示张强离家的距离。根据图象提供的信息，以下四个说法错误的是（ ）

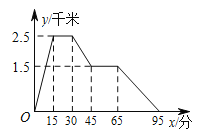
    A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟

    C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一个运输队承包了一家公司运送货物的业务，第一次运送18吨，派了1辆大卡车和5辆小卡车；第二次运送38吨，派了2辆大卡车和11辆小卡车，并且两次派的车都刚好装满。

    (1)两种车型的载重量各是多少吨？

    (2)若大卡车运送一次的费用为200元，小卡车运送一次的费用为60元，在第一次运送过程中怎样安排大小车辆,才能使费用最少?(直接写出派车方案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，CD⊥DA，DA⊥AB，∠1=∠2．试确定射线DF与AE的位置关系，并说明你的理由．

    某同学在解决上面问题时，准备三步走，请你完成他的步骤．

    (1)问题的结论：DF____AE．

    (2)思路要使DF_____AE，只要∠3=____．

    (3)说理过程：

    解：∵CD⊥DA，DA⊥AB，

    ∴∠CDA=∠DAB=________．( )

    又∵∠1=∠2，

    ∴∠CDA﹣∠2=____﹣____，( )

    即∠3=______，

    ∴DF_____AE．( )

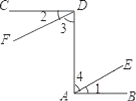
    查看答案和解析>>

    同步练习册答案