
【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
【答案】(1)见解析;(2) 当O运动到OA=OC处,四边形AECF是矩形.理由见解析.
【解析】
(1)由于CE平分∠BCA,那么有∠1=∠2,而MN∥BC,利用平行线的性质有∠1=∠3,等量代换有∠2=∠3,于OE=OC,同理OC=OF,于是OE=OF;
(2)OA=OC,那么可证四边形AECF是平行四边形,又CE、CF分别是∠BCA及其外角的角平分线,易证∠ECF是90°,从而可证四边形AECF是矩形.
(1)当点O运动到AC中点时,四边形AECF是矩形;理由如下:
如图所示:
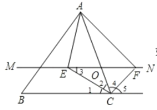
∵CE平分∠BCA,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO;
(2)当O运动到OA=OC处,四边形AECF是矩形.理由如下:
∵OA=OC,
∴四边形AECF是平行四边形,
∵CF是∠BCA的外角平分线,
∴∠4=∠5,
又∵∠1=∠2,
∴∠1+∠5=∠2+∠4,
又∵∠1+∠5+∠2+∠4=180°,
∴∠2+∠4=90°,
∴平行四边形AECF是矩形.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12
B.24
C.8
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一条抛物线,三位学生分别说出了它的一些性质:
甲说:对称轴是直线x=2;
乙说:与x轴的两个交点距离为6;
丙说:顶点与x轴的交点围成的三角形面积等于9,请你写出满足
上述全部条件的一条抛物线的解析式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小方格的边长 为 1,点 A、B、C 是格点.

(1)计算:AB= ;BC= ;AC= ;
(2)只用直尺(不带刻度)作出 AB 边上的高 CH(保留作图 痕迹)CH= ;
(3)只用直尺(不带刻度)作出 AC 边上的高 BG(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是

A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线a∥b,直线c与直线a、b分别相交于C、D两点,直线d与直线a、b分别相交于A、B两点,点P在直线AB上运动(不与A、B两点重合).
(1)如图1,当点P在线段AB上运动时,总有:∠CPD=∠PCA+∠PDB,请说明理由;
(2)如图2,当点P在线段AB的延长线上运动时,∠CPD、∠PCA、∠PDB之间有怎样的数量关系,并说明理由;
(3)如图3,当点P在线段BA的延长线上运动时,∠CPD、∠PCA、∠PDB之间又有怎样的数量关系(只需直接给出结论)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,线段![]() 直线
直线![]() ,垂足为
,垂足为![]() ,平移线段
,平移线段![]() ,使点
,使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点记为点
的对应点记为点![]() .
.

操作与思考:
(1)画出线段![]() 和直线
和直线![]() ;
;
(2)直线![]() 与
与![]() 的位置关系是_______,理由是:____________________________;
的位置关系是_______,理由是:____________________________;
线段![]() 与
与![]() 的数量关系是_______,理由是:____________________________.
的数量关系是_______,理由是:____________________________.
实践与应用:
(3)如图,等边![]() 和等边
和等边![]() 的面积分别为3和5,点
的面积分别为3和5,点![]() 、
、![]() 、
、![]() 在一直线上,则
在一直线上,则![]() 的面积是_____________.
的面积是_____________.

(4)如图,网格中每个小正方形的边长为1,请用三种不同方法,求出![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
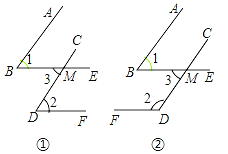
【题目】已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由.
(1)如图①,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(2)如图②,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(3)经过上述证明,我们可得出结论,如果一个角的两边与另一个角的两边分别平行,那么这两个角 ;
(4)若这两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com