
【题目】有一条抛物线,三位学生分别说出了它的一些性质:
甲说:对称轴是直线x=2;
乙说:与x轴的两个交点距离为6;
丙说:顶点与x轴的交点围成的三角形面积等于9,请你写出满足
上述全部条件的一条抛物线的解析式: .
【答案】y=﹣ ![]() (x﹣2)2+3或y=
(x﹣2)2+3或y= ![]() (x﹣2)2﹣3.
(x﹣2)2﹣3.
【解析】解:根据题意得:抛物线与x轴的两个交点的坐标为(﹣1,0),(5,0),顶点坐标为(2,3)或(2,﹣3),
设函数解析式为y=a(x﹣2)2+3或y=a(x﹣2)2﹣3;
把点(5,0)代入y=a(x﹣2)2+3得a=﹣ ![]() ;
;
把点(5,0)代入y=a(x﹣2)2﹣3得a= ![]() ;
;
∴满足上述全部条件的一条抛物线的解析式为y=﹣ ![]() (x﹣2)2+3或y=
(x﹣2)2+3或y= ![]() (x﹣2)2﹣3.
(x﹣2)2﹣3.
根据对称轴是直线x=2,与x轴的两个交点距离为6,所以与x轴的两个交点的坐标为(-1,0),(5,0),再根据顶点与x轴的交点围成的三角形面积等于9,可得顶点的纵坐标为±3,得顶点坐标为(2,3)或(2,-3),然后利用顶点式求得抛物线的解析式即可。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.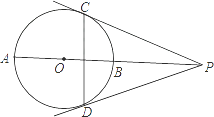
(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO= ![]() ,求PO的长.
,求PO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列填空.
如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.

证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD( ).
∴∠B=∠DCE( ).
又∵∠B=∠D(已知 ),
∴___________ ( 等量代换 ).
∴AD∥BE(内错角相等,两直线平行)
∴∠E=∠DFE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距10千米,上午9:00甲骑电动车从A地出发到B地,9:10乙开车从B地出发到A地,甲、乙两人距A 地距离y(千米)与甲所用的时间x(分)之间的关系如图所示。

(1)甲的速度是 千米/分。
(2)乙的速度是 千米/分,乙到达A地的时间是 。
(3)甲、乙两人相距4千米的时间是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→,…,根据这个规律,第2019个点的坐标为______.
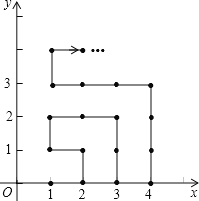
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为 . 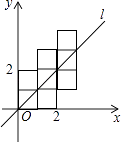
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com