
【题目】已知∠AOB=90°,OC为一条射线,OE,OF分别平分∠AOC,∠BOC,那么∠EOF 的度数为_____________.
【答案】45°或135°
【解析】
解答此题首先进行分类讨论,当OC是∠AOB里的一条射线时,根据题干条件求出一个值,当OC是∠AOB外的一条射线时,根据平分线的知识可以得到角之间的关系,进而求得∠EOF的大小.
解:①OC在∠AOB内部,
如图所示:

∵OE,OF分别平分∠AOC和∠BOC,∴∠COE=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,
∠BOC,
∴∠COE+∠COF=![]() ∠AOC+
∠AOC+![]() ∠BOC,
∠BOC,
即∠EOF=![]() ∠AOB,
∠AOB,
又∵∠AOB=90°,
∴∠EOF=45°;
②如图,

当OC在∠AOB外部时,
∵OE,OF分别平分∠AOC和∠BOC,
∴∠AOE=∠EOC=![]() ∠AOC,∠BOF=∠FOC=
∠AOC,∠BOF=∠FOC=![]() ∠BOC,
∠BOC,
∴∠EOF=∠EOC+∠FOC=(360°90°)÷2,
∴∠EOF=135°,
综上所述:∠EOF=45°或135°.
故答案为:45°或135°.


科目:初中数学 来源: 题型:
【题目】(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ![]() ≈1.414)( )
≈1.414)( )
A.34.14米
B.34.1米
C.35.7米
D.35.74米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于点(﹣1,0)和(3,0),与y轴交于点(0,﹣3)则此抛物线对此函数的表达式为( )
A.y=x2+2x+3
B.y=x2﹣2x﹣3
C.y=x2﹣2x+3
D.y=x2+2x﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一条抛物线,三位学生分别说出了它的一些性质:
甲说:对称轴是直线x=2;
乙说:与x轴的两个交点距离为6;
丙说:顶点与x轴的交点围成的三角形面积等于9,请你写出满足
上述全部条件的一条抛物线的解析式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD 中,点 E,F 分别在 AB,CD 上,且 AE=CF.

(1)求证:四边形 AECF 是平行四边形;
(2)直接写出 CE 与 AE 满足 时, AECF是矩形;
(3)直接写出 CE 与 AE 满足 时, AECF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小方格的边长 为 1,点 A、B、C 是格点.

(1)计算:AB= ;BC= ;AC= ;
(2)只用直尺(不带刻度)作出 AB 边上的高 CH(保留作图 痕迹)CH= ;
(3)只用直尺(不带刻度)作出 AC 边上的高 BG(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.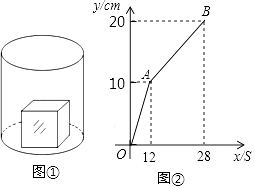
(1)正方体的棱长为cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com