
【题目】(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
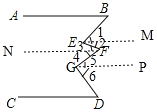
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?

【答案】(1)理由见解析
(2)AB∥CD.
(3)∠B+∠D+∠E=360°.
(4)∠B=∠D+∠E.
(5)∠E+∠G=∠B+∠F+∠D.
【解析】试题分析:已知AB∥CD,连接AB、CD的折线内折或外折,或改变E点位置、或增加折线的条数,通过适当地改变其中的一个条件,就能得出新的结论,给我们创造性的思考留下了极大的空间,解题的关键是过E点作AB(或CD)的平行线,把复杂的图形化归为基本图形.
试题解析:(1)理由:过点E作EF∥AB,
∴∠B=∠BEF.
∵CD∥AB,∴CD∥EF.∴∠D=∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠BED.
(2)若∠B+∠D=∠E,由EF∥AB,得∠B=∠BEF,
∵∠E=∠BEF+∠DEF=∠B+∠D,
∴∠D=∠DEF,∴EF∥CD,
∴AB∥CD;
(3) 若将点E移至图2所示位置,过E作EF∥AB,
∴∠BEF+∠B=180°,
∵EF∥CD,
∴∠D+∠DEF=180°,
∠B+∠D+∠E=360°.
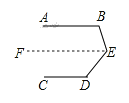
(4)∵AB∥CD,
∴∠B=∠BFD,
∵∠D+∠E=∠BFD,
∴∠D+∠E=∠B;

(5) 如图,作EM∥AB,FN∥AB,GP∥AB
∵AB∥CD,
∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D
∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D
∴∠1+∠2=∠E,5+∠6=∠G,∠3+∠4=∠F
∴E+∠G=∠B+∠F+∠D.


科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
若整数![]() 能被4整除,则称整数
能被4整除,则称整数![]() 为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。
为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。
(1)10到15之间的“完美数”是_______;
若![]() ,
,![]() 是整数,则
是整数,则![]() ________ “完美数”(填:“是”或“不是”);
________ “完美数”(填:“是”或“不是”);
(2)若任意四个连续的“完美数”中最小数的是4![]() (
(![]() 是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;
是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;
(3)当![]() 是正整数时,试说明:
是正整数时,试说明:![]() 一定是“完美数”.
一定是“完美数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从D点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网
B.球会过球网但不会出界
C.球会过球网并会出界
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.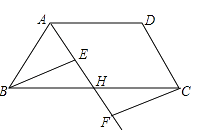
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
![]()
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)研究平面直角坐标系,我们可以发现一条重要的规律:若平面直角坐标系上有两个不同的点![]() 、
、![]() ,则线段AB的中点坐标可以表示为
,则线段AB的中点坐标可以表示为![]()

(简单应用)如图1,直线AB与y轴交于点![]() ,与x轴交于点
,与x轴交于点![]() ,过原点O的直线L将
,过原点O的直线L将![]() 分成面积相等的两部分,请求出直线L的解析式;
分成面积相等的两部分,请求出直线L的解析式;
(探究升级)小明发现“若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点”
如图2,在四边形ABCD中,对角线AC、BD相交于点O,![]() 试说明
试说明![]() ;
;
(综合运用)如图3,在平面直角坐标系中![]() ,
,![]() ,
,![]() ,若OC恰好平分四边形OACB的面积,求点C的坐标.
,若OC恰好平分四边形OACB的面积,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com