
【题目】阅读材料,回答问题:
若整数![]() 能被4整除,则称整数
能被4整除,则称整数![]() 为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。
为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。
(1)10到15之间的“完美数”是_______;
若![]() ,
,![]() 是整数,则
是整数,则![]() ________ “完美数”(填:“是”或“不是”);
________ “完美数”(填:“是”或“不是”);
(2)若任意四个连续的“完美数”中最小数的是4![]() (
(![]() 是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;
是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;
(3)当![]() 是正整数时,试说明:
是正整数时,试说明:![]() 一定是“完美数”.
一定是“完美数”.
【答案】(1)12,是;(2)是;(3)见解析.
【解析】
(1)10到15之间的数能被4整除的数只有12,可得10到15之间的“完美数”是12;(2)根据题意表示出这四个连续的“完美数”中最大数的是4(![]() +3),再求得这四个连续的“完美数”中最小数与最大数的积为
+3),再求得这四个连续的“完美数”中最小数与最大数的积为![]() ,由此即可解答;(3)因为
,由此即可解答;(3)因为![]() =
=![]() , n是正整数,即可判定
, n是正整数,即可判定![]() 和
和![]() 都是偶数,所以
都是偶数,所以![]() 能被4整除,结论得证.
能被4整除,结论得证.
(1)∵10到15之间的数能被4整除的数只有12,
∴10到15之间的“完美数”是12;
∵![]() =4mn(
=4mn(![]() ,
,![]() 是整数),4mn能被4整除,
是整数),4mn能被4整除,
∴![]() 是“完美数”;
是“完美数”;
故答案为:12,是;
(2)∵任意四个连续的“完美数”中最小数的是4![]() (
(![]() 是整数),
是整数),
∴这四个连续的“完美数”中最大数的是4(![]() +3),
+3),
∴这四个连续的“完美数”中最小数与最大数的积为4n·4(![]() +3)=
+3)=![]() ,
,
∵n是整数,
∴![]() 是偶数,
是偶数,
∴这四个连续的“完美数”中最小数与最大数的积是32的倍数;
(3)![]() =
=![]() ,
,
∵n是正整数,
∴![]() 和
和![]() 都是偶数,
都是偶数,
∴![]() 能被4整除,
能被4整除,
即![]() 是“完美数”.
是“完美数”.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,tan∠C= ![]() ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A.18cm2
B.12cm2
C.9cm2
D.3cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A,B的坐标分别为(﹣6,0),(4,0),点D在y轴上.

(1)求点C的坐标;
(2)求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
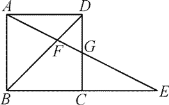
【题目】如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )
A. 6B. 8
C. 10D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=DC,AD=BC,E,F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( )

A. 150° B. 40° C. 80° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列结论:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BDF;④∠ABF=∠BCD,其中正确的有( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=90°,AB=4cm,BC=8cm,E、F是AD,DC的中点,连接EF、BE、BF,已知四边形ABCD的面积为36![]() ,△DEF的面积是△DAC面积的
,△DEF的面积是△DAC面积的![]() ,求△BEF的面积_____
,求△BEF的面积_____![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知∠1+∠2=180°,∠3=∠B,
求证:∠AED=∠ACB.

证明:∠1+∠2=180°(已知),∠1+∠4=180°( ),
∴∠2= ( ),
∴AB∥EF( ),
∴∠3= ( ),
∵∠3=∠B(已知),
∴∠B= (等量代换),
∴DE∥BC( ),
∴∠AED=∠ACB( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com