
【题目】如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列结论:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BDF;④∠ABF=∠BCD,其中正确的有( )

A. 4个B. 3个C. 2个D. 1个
【答案】C
【解析】
根据平行线的性质求出∠ACB=∠E,根据角平分线定义和平行线的性质求出∠ABF=∠CBF=∠ADC=∠EDC,推出BF∥DC,再根据平行线的性质判断即可.
∵BC∥DE,
∴∠ACB=∠E,∴①正确;
∵BC∥DE,
∴∠ABC=∠ADE,
∵BF平分∠ABC,DC平分∠ADE,
∴∠ABF=∠CBF=![]() ∠ABC,∠ADC=∠EDC=
∠ABC,∠ADC=∠EDC=![]() ∠ADE,
∠ADE,
∴∠ABF=∠CBF=∠ADC=∠EDC,
∴BF∥DC,
∴∠BFD=∠FDC,
∴根据已知不能推出∠ADF=∠CDF,∴②错误;③错误;
∵∠ABF=∠ADC,∠ADC=∠EDC,
∴∠ABF=∠EDC,
∵DE∥BC,
∴∠BCD=∠EDC,
∴∠ABF=∠BCD,∴④正确;
即正确的有2个,
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
若整数![]() 能被4整除,则称整数
能被4整除,则称整数![]() 为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。
为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。
(1)10到15之间的“完美数”是_______;
若![]() ,
,![]() 是整数,则
是整数,则![]() ________ “完美数”(填:“是”或“不是”);
________ “完美数”(填:“是”或“不是”);
(2)若任意四个连续的“完美数”中最小数的是4![]() (
(![]() 是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;
是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;
(3)当![]() 是正整数时,试说明:
是正整数时,试说明:![]() 一定是“完美数”.
一定是“完美数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店计划购进一批新的花束以满足市场需求,三款不同品种的花束,进价分别是A款180元/束,B款60元/束,C款120元/束。店铺在经销中,A款花束可赚20元/束,B款花束可赚10元/束,C款花束可赚12元/束。
(1)若商场用6000元同时购进两种不同款式的花束共40部,并恰好将钱用完,请你通过计算分析进货方案;
(2)在(1)的条件下,求盈利最多的进货方案;
(3)若该店铺同时购进三款花束共20束,共用去1800元,问这次店铺共有几种可能的方案?利润最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
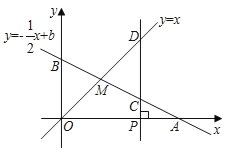
【题目】如图,已知函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,与函数
,与函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 的横坐标为2.在
的横坐标为2.在![]() 轴上有一点
轴上有一点![]() (其中
(其中![]() ),过点
),过点![]() 作
作![]() 轴的垂线,分别交函数
轴的垂线,分别交函数![]() 和
和![]() 的图象于点
的图象于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若四边形![]() 是平行四边形,求
是平行四边形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.
(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com