
����Ŀ��ij����ƻ�����һ���µĻ����������г��������ͬƷ�ֵĻ��������۷ֱ���A��180Ԫ/����B��60Ԫ/����C��120Ԫ/���������ھ����У�A�����20Ԫ/����B�����10Ԫ/����C�����12Ԫ/����
��1�����̳���6000Ԫͬʱ�������ֲ�ͬ��ʽ�Ļ�����40������ǡ�ý�Ǯ���꣬����ͨ�������������������
��2���ڣ�1���������£���ӯ�����Ľ���������
��3�����õ���ͬʱ�����������20��������ȥ1800Ԫ������ε��̹��м��ֿ��ܵķ�������������Ƕ���Ԫ��
���𰸡���1������������2��������.��3������4�ֿ��ܵķ��������������244Ԫ.
��������
��1���蹺��A�x����B�y����C�z��.������6000Ԫͬʱ�������ֲ�ͬ��ʽ�Ļ�����40������ǡ�ý�Ǯ���꣬������������ۣ��õ�������Ԫһ�η����飬��֮�ɵô𰸣�
��2������ÿ�ֻ�����������Լ�������ַ�������õ������ȽϾͿɵó�ӯ�����Ľ���������
��3�����������ж�Ԫһ�η��̣��������ȡֵ��Χ���������⣬�����бȽϿɵó���.
��1���蹺��A�x����B�y����C�z��.�������������ַ�����
��ֻ����A�x����B�y����������ɵ�
![]() �����
�����![]() ��
��
��ֻ����A�x����C�z����������ɵ�
![]() �����
�����![]() ��
��
��ֻ����B�y����C�z����������ɵ�
![]() �����
�����![]() ��(y�Ǹ�ֵ������ȥ)
��(y�Ǹ�ֵ������ȥ)
���Թ������ַ�����
����һ�� ����A�30����B�10����
������ ������A�20����C�20�� .
��2������һ������30��20+10��10��700��Ԫ��
������������20��20+20��12��640��Ԫ��
700��640
����ӯ�����Ľ��������Ƿ���һ��������A�30����B�10��.
��3���蹺��A�a����B�b������C�(20-a-b)��,���������
180a+60b+120(20-a-b)=1800
������b=a+10
�൱A�����a��ʱ��B�Ϊ(a+10)����C�(10-2a)��.
�������֪���ֻ���������������������a��1��2��3��4.
���ֻ��������������б����£�
A | B | C | ���� |
1 | 11 | 8 | 226 |
2 | 12 | 6 | 232 |
3 | 13 | 4 | 238 |
4 | 14 | 2 | 244 |
����ε��̹���4�ֿ��ܵķ��������������244Ԫ.


 ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����н����̣���ͼ�ף�AB��CD��̽����APC���BAP����PCD֮��Ĺ�ϵ��

�⣺����P��PE��AB��
��AB��CD��
��PE��AB��CD��ƽ����ͬһ��ֱ�ߵ�����ֱ����ƽ�У���
���1+��A=180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�������
��2+��C=180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�������
���1+��A+��2+��C=360�㣮
�֡ߡ�APC=��1+��2��
���APC+��A+��C=360�㣮
��ͼ�Һ�ͼ����AB��CD����������������ֱ�̽����ͼ�С�APC���BAP����PCD֮��Ĺ�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱߡ�ABC�У�AB =24 cm������AG��BC����E�ӵ�A����������AG��3cm/s���ٶ��˶���ͬʱ��F�ӵ�B����������BC��5cm/s���ٶ��˶������E�˶���ʱ��Ϊt��s����

��1������F���߶�BC���˶�ʱ��CF= cm������F���߶�BC���ӳ������˶�ʱ��CF= cm�����ú�t��ʽ�ӱ�ʾ����
��2���������˶������У����Ե�A��C��E��FΪ������ı�����ƽ���ı���ʱ����t��ֵ��
��3����t = sʱ��E��F�����ľ�����С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �����㣬����
�����㣬����![]() ��
��![]() .
.

��1����˵����![]() ��
��
��2�����![]() ��
��![]() ����
����![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BC��DE��BFƽ�֡�ABC��DCƽ�֡�ADE�������н��ۣ��١�ACB����E����DFƽ�֡�ADC���ۡ�BFD����BDF���ܡ�ABF����BCD��������ȷ����( )

A. 4��B. 3��C. 2��D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
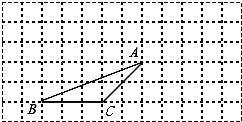
����Ŀ����ͼ����ABC�Ķ��㶼�ڷ���ֽ�ĸ���ϣ�����ABC����ƽ��4��������ƽ��2������ÿ�����ӵı߳�Ϊ1����λ���ȡ�
����ͼ�л���ƽ�ƺ�ġ�A��B��C����
��������AA����CC�������������߶εĹ�ϵ�� ��
������ABC�ĸ�AD�������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD��BC���ϵĸߣ�AE��BF�ֱ��ǡ�BAC,��ABC��ƽ���ߣ���DAC=20��
������ABC=60��,���EAD�Ķ�����
��AE��BF�ཻ�ڵ�G�����AGB�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ǧ���˶�Ա��Ǧ��ĸ߶�y��m����ˮƽ����x��m��֮��ĺ�����ϵʽ��y=�� ![]() x2+
x2+ ![]() x+
x+ ![]() ������˶�Ա�˴���Ǧ��ijɼ��ǣ� ��
������˶�Ա�˴���Ǧ��ijɼ��ǣ� ��
A.6m
B.12m
C.8m
D.10m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ6����֪��ͷ�ķ�����ˮ���ķ���һ����ͧ�ӽ��ĵ����Ҳ�A����������3Сʱ����B����ּ���˳������2.5Сʱ��C�㣬�ܹ�������208ǧ�ף���֪ˮ�����ٶ���2ǧ��/ʱ��
��1������ͧ�ھ�ˮ�е��ٶȡ�
��2������AC���ڽ��ţ���ͧ��ͬ�����ٶ���ԭ·���ع������ʱ�䣿���������һλС����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com