
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.

解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠APC与∠BAP、∠PCD之间的关系.
【答案】见解析
【解析】
图乙,过P作PE∥AB,求出AB∥PE∥CD,根据平行线的性质得出∠A=∠APE,∠C=∠CPE,即可求出答案;
图丙,根据平行线的性质得出∠PCD=∠POB,根据三角形外角性质求出∠POB=∠PAB+∠APC,即可求出答案.
解:图乙,∠APC=∠A+∠C,
理由是:
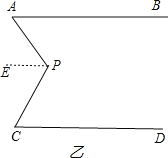
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠A=∠APE,∠C=∠CPE,
∴∠APC=∠APE+∠CPE=∠A+∠C;
图丙,∠APC=∠PCD-∠PAB,
理由是:∵AB∥CD,
∴∠PCD=∠POB,
∵∠POB=∠PAB+∠APC,
∴∠APC=∠POB-∠PAB=∠PCD-∠PAB.


科目:初中数学 来源: 题型:
【题目】如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y= ![]() (x>0)的图象经过AB的中点F和DE的中点G,则k的值为 .
(x>0)的图象经过AB的中点F和DE的中点G,则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边CD恰好与边AB平行.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了选择1名车工参加加工直径为10 mm的精密零件的技术比赛,随机抽取甲、乙两名车工加工的5个零件,现测得的结果如下表,请你比较![]() 、
、![]() 的大小( )
的大小( )

A. ![]() >
>![]()
B. ![]() =
=![]()
C. ![]() <
<![]()
D. ![]() ≤
≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ![]() ;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= .
;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= . 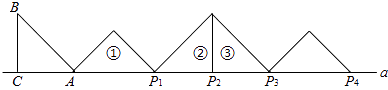
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:

(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2、3中的a= ,b= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芳芳同学手中有一块长方形纸板和一块正方形纸板,其中长方形纸板的长为3 dm,宽为2 dm,且两块纸板的面积相等.
(1)求正方形纸板的边长(结果保留根号).
(2)芳芳能否在长方形纸板上截出两个完整的,且面积分别为2 dm2和3 dm2的正方形纸板?判断并说明理由.(提示:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
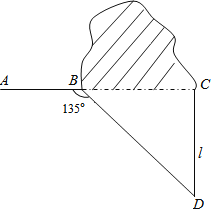
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com