
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ![]() ;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= .
;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= . 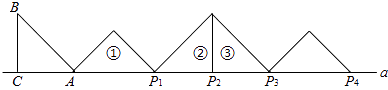
【答案】1343+672 ![]()
【解析】解:AP1= ![]() ,AP2=1+
,AP2=1+ ![]() ,AP3=2+
,AP3=2+ ![]() ;
;
AP4=2+2 ![]() ;AP5=3+2
;AP5=3+2 ![]() ;AP6=4+2
;AP6=4+2 ![]() ;
;
AP7=4+3 ![]() ;AP8=5+3
;AP8=5+3 ![]() ;AP9=6+3
;AP9=6+3 ![]() ;
;
∵2015=3×671+2,
∴AP2013=(2013﹣671)+671 ![]() =1342+671
=1342+671 ![]() ,
,
∴AP2014=1342+671 ![]() +
+ ![]() =1342+672
=1342+672 ![]() ,
,
∴AP2015=1342+672 ![]() +1=1343+672
+1=1343+672 ![]() .
.
所以答案是:1343+672 ![]() .
.
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图,将连续的奇数![]() ,
,![]() ,
,![]() ,
,![]() ...按图1中的方式排成一个数表,用一个十字框框住
...按图1中的方式排成一个数表,用一个十字框框住![]() 个数,这样框出的任意
个数,这样框出的任意![]() 个数中,四个分支上的数分别用
个数中,四个分支上的数分别用![]() 、
、![]() 、
、![]() 、
、![]() 表示,如图2所示。
表示,如图2所示。

(1)计算:若十字框中间的数为![]() ,则
,则![]() ______________;
______________;
(2)发现:移动十字框,比较![]() 与中间的数
与中间的数![]() .猜想:十字框中
.猜想:十字框中![]() 、
、![]() 、
、![]() 、
、![]() 的和是中间的数
的和是中间的数![]() 的___________________;
的___________________;
(3)验证:用含![]() 的式子表示
的式子表示![]() 、
、![]() 、
、![]() 、
、![]() ,并利用整式运算验证(2)中猜想的正确性;
,并利用整式运算验证(2)中猜想的正确性;
(4)应用:设![]() ,判断
,判断![]() 的值能否等于
的值能否等于![]() ,请说明理由.
,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ACB=90,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点按顺时针方向旋转90后得CE,连接EF.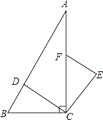
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).
(2)若∠B=60,AB=3,求⊙P的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= ![]() 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.

解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠APC与∠BAP、∠PCD之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“让所有的孩子都能上得起来,都能上好学”,国家自2007年起出台了一系列“资助贫困学生”的政策,其中包括向经济困难的学生免费提供教科书的政策.为确保这项工作顺利实施,学校需要调查学生的家庭情况.以下是某市城郊一所中学甲、乙两个班的调查结果,整理成表(一)和图(一):
| 城镇户口 (非低保) | 农村户口 | 城镇低保 | 总人数 |
甲班/人 | 20 | 5 |
| |
乙班/人 | 28 | 22 | 4 |
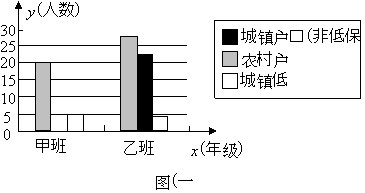
(1)将表(一)和图(一)中的空缺部分补全;
(2)现要预定2009年下学期的教科书,全额100元.若农村户口学生可全免,城镇低保的学生可减免![]() 城镇户口(非低保)学生全额交费.求乙班应交书费多少元?甲班受到国家资助教科书的学生占全班人数的百分比是多少?
城镇户口(非低保)学生全额交费.求乙班应交书费多少元?甲班受到国家资助教科书的学生占全班人数的百分比是多少?
(3)五四青年节时,校团委免费赠送给甲、乙两班若干册科普类、文学类及艺术类三种图书,其中文学类图书有15册,三种图书所占比例如图(二)所示,求艺术类图书共有多少册?
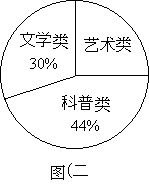
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
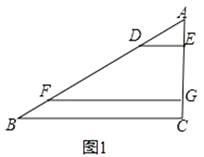
(1)如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= , ![]() = .
= . 
(2)如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.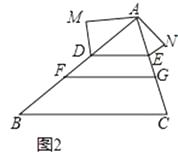
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com