
【题目】综合题
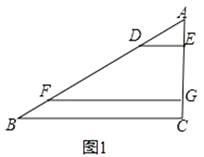
(1)如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= , ![]() = .
= . 
(2)如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.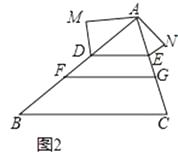
【答案】
(1)2,2
(2)证明:∵DE∥FG∥BC,
∴ ![]() ,
,
∵AM=BF,MD=DF,AN=GC,NE=EG,
∴ ![]() ,
,
∴△ADM∽△AEN,
∴∠M=∠N
【解析】(1)解:∵DE∥FG,
∴ ![]() ,
,
∵AD=2,AE=1,DF=4,
∴EG=2,
∴AF=AD+DF=6,AG=AE+EG=3,
∵DE∥FG∥BC,
∴ ![]() =2;
=2;
故答案为:2,2;
(1)根据平行线分线段成比例定理得出:AD∶DF=AE∶EG ,从而得出EG的长,进而得出AF,AG的长 ,再根据平行线分线段成比例定理得出FB∶GC=AF∶AG ,从而得出答案;
(2)根据平行线分线段成比例定理得出:AD∶AE=DF∶EG=FB∶GC ,又AM=BF,MD=DF,AN=GC,根据等量代换得出AD∶AE=MD∶NE=AM∶AN ,从而判断出△ADM∽△AEN,根据相似三角形对应角相等得出结论。


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ![]() ;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= .
;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= . 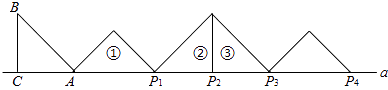
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在A、B两家超市发现他看中的随身听和书包的单价都相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.
(1)求小明看中的随身听和书包单价各是多少元?
(2)假日期间商家开展促销活动,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(购物满100元返购物券30元,购物满200元返购物券60元,以此类推;不足100元不返券,购物券可通用).小明只有400元钱,他能买到一只随身听和一个书包吗?若能,选择在哪一家购买更省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
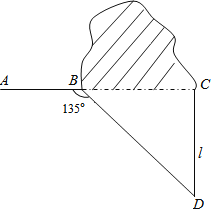
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2+2(k﹣3)x+(k﹣3)的图象开口向上,且k为整数,且该抛物线与x轴有两个交点(a,0)和(b,0).一次函数y1=(k﹣2)x+m与反比例函数y2= ![]() 的图象都经过(a,b).
的图象都经过(a,b).
(1)求k的值;
(2)求一次函数和反比例函数的解析式,并直接写出y1>y2时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com