
【题目】小明同学在A、B两家超市发现他看中的随身听和书包的单价都相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.
(1)求小明看中的随身听和书包单价各是多少元?
(2)假日期间商家开展促销活动,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(购物满100元返购物券30元,购物满200元返购物券60元,以此类推;不足100元不返券,购物券可通用).小明只有400元钱,他能买到一只随身听和一个书包吗?若能,选择在哪一家购买更省钱.
【答案】(1)随身听和书包的单价分别是360元和92元;(2)详见解析.
【解析】
(1)设书包的单价为x元,随身听的单价为y元,根据随身听和书包单价之和是452元可以列出方程x+y=452,根据随身听的单价比书包单价的4倍少8元可以列出方程y=4x-8,联立两个方程组成方程组即可解决问题;
(2)分别根据销售A、B两个超市的销售方案计算出所需要的钱即可作出判断.
解:(1)设书包的单价为x元,随身听的单价为y元,
根据题意,得![]() 解得
解得![]()
答:随身听和书包的单价分别是360元和92元.
(2)在超市A购买随身听与书包各一件需花费现金:452×80%=361.6(元)
∵361.6<400,
∴可以选择超市A购买,
在超市B可先花费现金360元购买随身听,再利用得到的90元返券,
加上2元现金购买书包,总计共花费现金362(元),
∵362<400,
∴也可以选择在超市B购买.
∵362>361.6,
∴在超市A购买更省钱.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ACB=90,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点按顺时针方向旋转90后得CE,连接EF.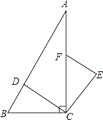
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“让所有的孩子都能上得起来,都能上好学”,国家自2007年起出台了一系列“资助贫困学生”的政策,其中包括向经济困难的学生免费提供教科书的政策.为确保这项工作顺利实施,学校需要调查学生的家庭情况.以下是某市城郊一所中学甲、乙两个班的调查结果,整理成表(一)和图(一):
| 城镇户口 (非低保) | 农村户口 | 城镇低保 | 总人数 |
甲班/人 | 20 | 5 |
| |
乙班/人 | 28 | 22 | 4 |
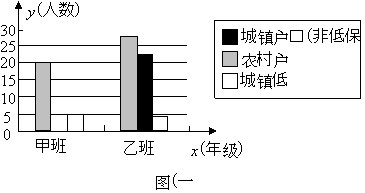
(1)将表(一)和图(一)中的空缺部分补全;
(2)现要预定2009年下学期的教科书,全额100元.若农村户口学生可全免,城镇低保的学生可减免![]() 城镇户口(非低保)学生全额交费.求乙班应交书费多少元?甲班受到国家资助教科书的学生占全班人数的百分比是多少?
城镇户口(非低保)学生全额交费.求乙班应交书费多少元?甲班受到国家资助教科书的学生占全班人数的百分比是多少?
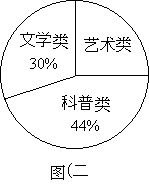
(3)五四青年节时,校团委免费赠送给甲、乙两班若干册科普类、文学类及艺术类三种图书,其中文学类图书有15册,三种图书所占比例如图(二)所示,求艺术类图书共有多少册?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市投入15000元资金购进![]() 、
、![]() 两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
类别/单价 | 成本价(元/箱) | 销售价(元/箱) |
A品牌 | 20 | 32 |
B品牌 | 35 | 50 |
(1)该大型超市购进![]() 、
、![]() 品牌矿泉水各多少箱?
品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
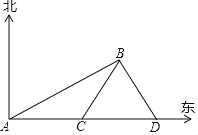
【题目】如图,“中国海监50”于上午11时30分在南海海域A处巡逻,观测到岛礁B在北偏东60°,该船以每小时10海里的速度向正东航行到C处,观测岛礁B在北偏东30°,继续向正东航行到D处时,再观测到岛礁B在北偏西30°,当海监船到达C处时恰与岛礁B相距20海里,请你分别确定“中国海监50”从A处到达C处和D处所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足若 ![]() =
= ![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3. 
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求tan∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
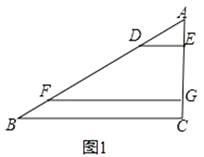
(1)如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= , ![]() = .
= . 
(2)如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.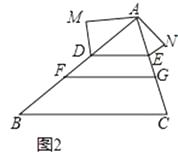
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AF∥DE,B为AF上一点,∠ABC=60°,交ED于C,CM平分∠BCE,∠MCN=90°.
(1)求∠DCN的度数;
(2)若∠CBF的平分线交CN于N,求证:BN∥CM.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com