
【题目】已知二次函数y=kx2+2(k﹣3)x+(k﹣3)的图象开口向上,且k为整数,且该抛物线与x轴有两个交点(a,0)和(b,0).一次函数y1=(k﹣2)x+m与反比例函数y2= ![]() 的图象都经过(a,b).
的图象都经过(a,b).
(1)求k的值;
(2)求一次函数和反比例函数的解析式,并直接写出y1>y2时,x的取值范围.
【答案】
(1)解:由题意得,抛物线与x轴有两个交点,
令y=0,即kx2+2(k﹣3)x+(k﹣3)=0,
则△=4(k﹣3)2﹣4k(k﹣3)>0,
解得,k<3,
∵二次函数的图象开口向上,故k>0,
又∵k为整数,k﹣2≠0,
∴k=1;
(2)解:由(1)得,y=x2﹣4x﹣2,
令x2﹣4x﹣2=0得x=2+ ![]() 或x=2﹣
或x=2﹣ ![]() ,
,
∴a+b=4,ab=﹣2,
把(a,b)代入y1=﹣x+m, ![]() 得,m=a+b=4,n=ab=﹣2
得,m=a+b=4,n=ab=﹣2
∴一次函数的表达式为y1=﹣x+4,
∴反比例函数的表达式为y2=﹣ ![]() ,
,
当y1>y2时,x<2﹣ ![]() 或0<x<2+
或0<x<2+ ![]()
【解析】(1)由抛物线与x轴有两个交点得出△=4(k﹣3)2﹣4k(k﹣3)>0,解得,k<3,又二次函数的图象开口向上,故k>0,又k为整数,k﹣2≠0,从而得出K=1 ;
(2)首先利用抛物线与x轴的交点得出其交点的横坐标,进而求出a+b=4,ab=﹣2,然后求出m,n的值,从而得出一次函数及反比例函数的解析式,画出草图,根据图像要当y1>y2时,自变量的值,主要能清楚谁大谁小,谁大就写谁的图像在上方时的自变量的取值即可。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】综合题
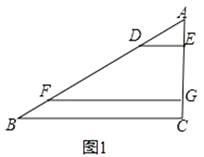
(1)如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= , ![]() = .
= . 
(2)如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.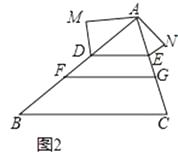
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AF∥DE,B为AF上一点,∠ABC=60°,交ED于C,CM平分∠BCE,∠MCN=90°.
(1)求∠DCN的度数;
(2)若∠CBF的平分线交CN于N,求证:BN∥CM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尝试探究并解答:
(1)为了求代数式x2+2x+3的值,我们必须知道x的值,若x=1,则这个代数式的值为 ;若x=2,则这个代数式的值为 ,可见,这个代数式的值因x的取值不同而 (填“变化”或“不变”).尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)本学期我们学习了形如a2+2ab+b2及a2﹣2ab+b2的式子,我们把这样的多项式叫做“完全平方式”在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式同样地,把一个多项式进行部分因式分解可以解决代数式的最大(或最小)值问题例如:x2+2x+3=(x2+2x+1)+2=(x+1)2+2,因为(x+1)2≥0,所以(x+1)2+2≥2,所以这个代数式x2+2x+3有最小值是2,这时相应的x的值是 .
(3)猜想:①4x2﹣12x+13的最小值是 ;
②﹣x2﹣2x+3有 值(填“最大”或“最小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
.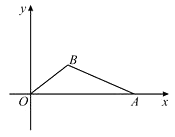
(1)①在图中,求作△ABO的外接圆;(尺规作图,不写作法但需保留作图痕迹);②求点B的坐标与cos∠BAO的值;
(2)若A,O位置不变,将点B沿 ![]() 轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中有这样一道题,原文是:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几何步及之?”意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步(两人的步长相同).走路慢的人先走100步,走路快的人要走多少步才能追上走路慢的人(两人走的路线相同)?试求解这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB. 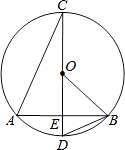
(1)求证:△AEC∽△DEB;
(2)若CD⊥AB,AB=8,DE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知A( ![]() ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y= ![]() 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A.( ![]() ,0)
,0)
B.(1,0)
C.( ![]() ,0)
,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com