
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
.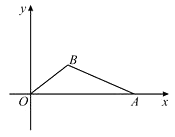
(1)①在图中,求作△ABO的外接圆;(尺规作图,不写作法但需保留作图痕迹);②求点B的坐标与cos∠BAO的值;
(2)若A,O位置不变,将点B沿 ![]() 轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
【答案】
(1)解:①如图所示:
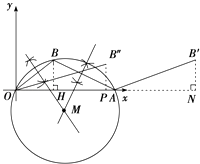
②作BH⊥OA,垂足为H,
在Rt△OHB中,∵BO=10,sin∠BOA= ![]() ,
,
∴BH=6,
∴OH=8,∴点B的坐标为(8,6),
∵OA=20,OH=8,∴AH=12,
在Rt△AHB中,∵BH=6,
∴AB= ![]() =6
=6 ![]()
∴cos∠BAO= ![]() =
= ![]()
(2)解:①当BO=AB时,∵AO=20,∴OH=10,
∴点B沿x轴正半轴方向平移2个单位,
②当AO=AB′时,∵AO=20,∴AB′=20,
过B′作B′N⊥x轴,
∵点B的坐标为(8,6),
∴B′N=6,∴AN= ![]() =2
=2 ![]() .
.
∴点B沿x轴正半轴方向平移(2 ![]() +12)个单位,
+12)个单位,
③当AO=OB″时,
∵AO=20,
∴OB″=20,
过B″作B″P⊥x轴.
∵B的坐标为(8,6),
∴B″P=6,
∴OP= ![]() =2
=2 ![]() ,
,
∴点B沿x轴正半轴方向平移(2 ![]() ﹣8)个单位,
﹣8)个单位,
综上所述当点B沿x轴正半轴方向平移2个单位、(2 ![]() +12)个单位,或(2
+12)个单位,或(2 ![]() ﹣8)个单位时,△ABO为等腰三角形
﹣8)个单位时,△ABO为等腰三角形
【解析】(1)作出BO和AB的垂直平分线,两线交点就是外接圆圆心,以交点为圆心,交点到O的距离为半径画圆即可;
(2)作BH⊥OA,垂足为H首先根据sin∠BOA及BO=10计算出B点坐标,然后根据勾股定理求出AB长,可得cos∠BAO;
(3)分三种情况进行计算,①当BO=AB时,②当AO=AB′时,③当AO=OB″时,,因为点B是沿x轴正半轴方向平移,因此B点纵坐标不变,依次利用勾股定理求出其横坐标即可。


科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
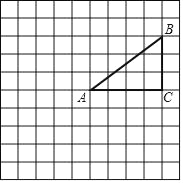
【题目】 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB'C′;
(2)画出△AB′C′向左平移4格后的△A′B″C″;
(3)计算线段AB在变换到AB′的过程中扫过区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
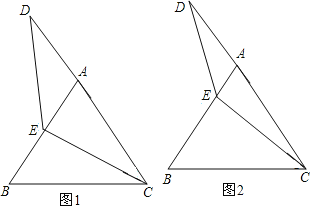
【题目】等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题:
(1)如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:AD BE;
(2)如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2+2(k﹣3)x+(k﹣3)的图象开口向上,且k为整数,且该抛物线与x轴有两个交点(a,0)和(b,0).一次函数y1=(k﹣2)x+m与反比例函数y2= ![]() 的图象都经过(a,b).
的图象都经过(a,b).
(1)求k的值;
(2)求一次函数和反比例函数的解析式,并直接写出y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )

A.①③B.②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何测得距离?
一位战士的测量方法是:面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。这是为什么呢?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com