练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠B=90°，∠A=30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是 ．

    【答案】
    【解析】解：如图所示，设BC=x，

    ∵在Rt△ABC中，∠B=90°，∠A=30°，

    ∴AC=2BC=2x，AB= BC= x，

    根据题意得：AD=BC=x，AE=DE=AB= x，

    如图，作EM⊥AD于M，则AM= AD= x，

    在Rt△AEM中，cos∠EAD= = = ，

    故答案为： ．

    设BC=x，由含30°角的直角三角形的性质得出AC=2BC=2x，求出AB= x，根据题意得出AD=BC=x，AE=DE=AB= x，作EM⊥AD于M，由等腰三角形的性质得出AM= x，在Rt△AEM中，由三角函数的定义即可得出结果．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足若 = ，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．
    （1）求证：△ADF∽△AED；
    （2）求FG的长；
    （3）求tan∠E的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知平行四边形ABCD中，AB=5, AE平分∠DAB交BC所在直线于点E，CE=2,则AD=_______；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AF∥DE，B为AF上一点，∠ABC＝60°，交ED于C，CM平分∠BCE，∠MCN＝90°．

    （1）求∠DCN的度数；

    （2）若∠CBF的平分线交CN于N，求证：BN∥CM．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

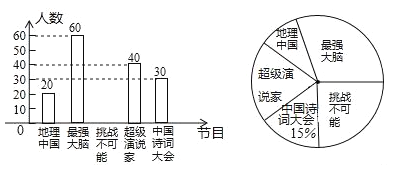
    【题目】我市某中学为了了解孩子们对《中国诗词大会》、《挑战不可能》、《最强大脑》、《超级演说家》、《地理中国》五种电视节目的喜爱程度，随机在七、八、九年级抽取了部分学生进行调查（每人只能选择一种喜爱的电视节目），并将获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据两幅统计图中的信息回答下列问题：

    （1）本次调查中共抽取了　 　名学生．

    （2）补全条形统计图．

    （3）在扇形统计图中，喜爱《地理中国》节目的人数所在的扇形的圆心角是　 　度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】尝试探究并解答：

    （1）为了求代数式x2+2x+3的值，我们必须知道x的值，若x＝1，则这个代数式的值为　 　；若x＝2，则这个代数式的值为　 　，可见，这个代数式的值因x的取值不同而　 　（填“变化”或“不变”）．尽管如此，我们还是有办法来考虑这个代数式的值的范围．

    （2）本学期我们学习了形如a2+2ab+b2及a2﹣2ab+b2的式子，我们把这样的多项式叫做“完全平方式”在运用完全平方公式进行因式分解时，关键是判断这个多项式是不是一个完全平方式同样地，把一个多项式进行部分因式分解可以解决代数式的最大（或最小）值问题例如：x2+2x+3＝（x2+2x+1）+2＝（x+1）2+2，因为（x+1）2≥0，所以（x+1）2+2≥2，所以这个代数式x2+2x+3有最小值是2，这时相应的x的值是　 　．

    （3）猜想：①4x2﹣12x+13的最小值是　 　；

    ②﹣x2﹣2x+3有　 　值（填“最大”或“最小”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标平面中，O为原点，点A的坐标为（20，0），点B在第一象限内，BO＝10，sin∠BOA＝ ．

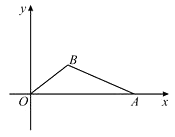
    （1）①在图中，求作△ABO的外接圆；（尺规作图，不写作法但需保留作图痕迹）;②求点B的坐标与cos∠BAO的值；
    （2）若A，O位置不变，将点B沿 轴正半轴方向平移使得△ABO为等腰三角形，请直接写出平移距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国古代数学著作《九章算术》中有这样一道题，原文是：“今有善行者行一百步，不善行者行六十步，今不善行者先行一百步，善行者追之，问几何步及之？”意思是：同样时间段内，走路快的人能走100步，走路慢的人只能走60步（两人的步长相同）．走路慢的人先走100步，走路快的人要走多少步才能追上走路慢的人（两人走的路线相同）？试求解这个问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

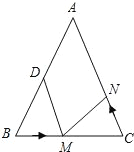
    【题目】如图，已知△ABC中，AB＝AC＝12厘米，BC＝8厘米，点D为AB的中点，如果点M在线段BC上以2厘米/秒的速度由B点向C点运动，同时，点N在线段CA上由C点向A点运动，若使△BDM与△CMN全等，则点N的运动速度应为_____厘米/秒．

    查看答案和解析>>

    同步练习册答案