
【题目】尝试探究并解答:
(1)为了求代数式x2+2x+3的值,我们必须知道x的值,若x=1,则这个代数式的值为 ;若x=2,则这个代数式的值为 ,可见,这个代数式的值因x的取值不同而 (填“变化”或“不变”).尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)本学期我们学习了形如a2+2ab+b2及a2﹣2ab+b2的式子,我们把这样的多项式叫做“完全平方式”在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式同样地,把一个多项式进行部分因式分解可以解决代数式的最大(或最小)值问题例如:x2+2x+3=(x2+2x+1)+2=(x+1)2+2,因为(x+1)2≥0,所以(x+1)2+2≥2,所以这个代数式x2+2x+3有最小值是2,这时相应的x的值是 .
(3)猜想:①4x2﹣12x+13的最小值是 ;
②﹣x2﹣2x+3有 值(填“最大”或“最小”).
【答案】(1)6,11,变化;(2)﹣1;(3)①4;②最大.
【解析】
(1)把x的值代入计算即可.
(2)根据非负数的性质即可解决问题.
(3)利用配方法即可解决问题.
(1)当x=1时,x2+2x+3=1+2+3=6.
当x=2时,x2+2x+3=4+4+3=11,这个代数式的值因x的取值不同而变化.
故答案为:6,11,变化.
(2)∵x2+2x+3=(x2+2x+1)+2=(x+1)2+2,∴当x=﹣1时,这个代数式的值的最小值为2.
故答案分别为:﹣1.
(3)①∵4x2﹣12x+13=4(x﹣![]() )2+4,∴x=
)2+4,∴x=![]() 时,代数式的最小值为4;
时,代数式的最小值为4;
②∵﹣x2﹣2x+3=﹣(x+1)2+4,∴x=﹣1时,代数式的最大值为4.
故答案为:4,最大.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
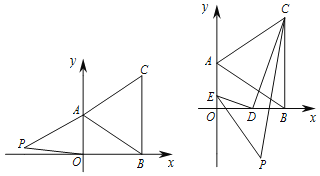
【题目】在下面直角坐标系中,已知A(0,a)、B(b,0)、C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0.
(1)a= ;b= ;c= ;
(2)在第二象限内,是否存在点P(m,![]() ),使四边形ABOP的面积与△ABC的面积相等?若存在,求出点m的值;若不存在,请说明理由;
),使四边形ABOP的面积与△ABC的面积相等?若存在,求出点m的值;若不存在,请说明理由;
(3)D为线段OB上一动点,连接CD,过D作DE⊥CD交y轴于点E,EP、CP分别平分∠DEO和∠DCB,当点D在OB上运动的过程中,∠P的度数是否变化,若不变,请求出∠P的度数;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
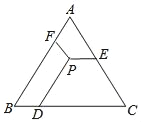
【题目】 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
A. 18B. 9![]()
C. 6D. 条件不够,不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2+2(k﹣3)x+(k﹣3)的图象开口向上,且k为整数,且该抛物线与x轴有两个交点(a,0)和(b,0).一次函数y1=(k﹣2)x+m与反比例函数y2= ![]() 的图象都经过(a,b).
的图象都经过(a,b).
(1)求k的值;
(2)求一次函数和反比例函数的解析式,并直接写出y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,4),B(6,4),将点A向右平移两个单位得到点C,将点A向下平移3个单位得到点D.

(1)依题意在下图中补全图形并直接写出三角形ABD的面积;
(2)点E是y轴上的点A下方的一个动点,连接EC,直线EC交线段BD于点F,若△DEF的面积等于三角形ACF面积的2倍.请画出示意图并求出E点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com