
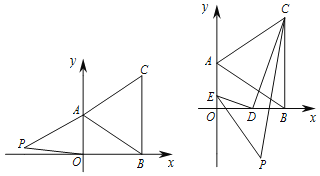
【题目】在下面直角坐标系中,已知A(0,a)、B(b,0)、C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0.
(1)a= ;b= ;c= ;
(2)在第二象限内,是否存在点P(m,![]() ),使四边形ABOP的面积与△ABC的面积相等?若存在,求出点m的值;若不存在,请说明理由;
),使四边形ABOP的面积与△ABC的面积相等?若存在,求出点m的值;若不存在,请说明理由;
(3)D为线段OB上一动点,连接CD,过D作DE⊥CD交y轴于点E,EP、CP分别平分∠DEO和∠DCB,当点D在OB上运动的过程中,∠P的度数是否变化,若不变,请求出∠P的度数;若变化,请说明理由.
【答案】(1)2,3,4;(2)存在,m=﹣3;(3)∠P的度数不变,∠P=45°,理由见解析
【解析】
(1)根据非负数的性质解答即可;
(2)根据四边形ABOP的面积=△ABO的面积+△APO的面积可得关于m的方程,解方程即得答案;
(3)易得BC∥y轴,过点P作PF∥BC,过点D作DM∥BC,易证∠P=∠OEP+∠PCB,∠EDC=∠OED+∠DCB,则可得∠P=![]() ∠EDC,进而可得结论.
∠EDC,进而可得结论.
解:(1)∵|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0,
∴a﹣2=0,b﹣3=0,c﹣4=0,
解得:a=2,b=3,c=4;
故答案为:2;3;4.
(2)∵a=2,b=3,c=4,
∴A(0,2),B(3,0),C(3,4),
∴OA=2,OB=3,
∵S△ABO=![]() ×2×3=3,S△APO=
×2×3=3,S△APO=![]() ×2×(﹣m)=﹣m,
×2×(﹣m)=﹣m,
∴S四边形ABOP=S△ABO+S△APO=3+(﹣m)=3﹣m.
∵S△ABC=![]() ×4×3=6,
×4×3=6,
∴S四边形ABOP=S△ABC=3﹣m=6,
∴m=﹣3,
∴存在点P(﹣3,![]() ),使S四边形ABOP=S△ABC.
),使S四边形ABOP=S△ABC.
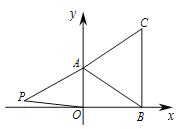
(3)∠P的度数不变,∠P=45°,理由如下:
∵B(b,0)、C(b,c)的横坐标相同,
∴BC∥y轴,
过点P作PF∥BC,如图,

∴PF∥y轴,
∴∠OEP=∠EPF,∠PCB=∠FPC,
∴∠EPC=∠EPF+∠FPC=∠OEP+∠PCB,
过点D作DM∥BC,
同理可得∠EDC=∠OED+∠DCB,
∵EP、CP分别平分∠DEO和∠DCB,
∴∠OEP=![]() ∠OED,∠PCB=
∠OED,∠PCB=![]() ∠DCB,
∠DCB,
∴∠EPC=![]() =
=![]() (∠OED+∠DCB)=
(∠OED+∠DCB)=![]() ∠EDC,
∠EDC,
∵DE⊥CD,∴∠EDC=90°,
∴∠EPC=![]() ×90°=45°.
×90°=45°.


科目:初中数学 来源: 题型:
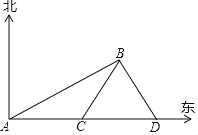
【题目】如图,“中国海监50”于上午11时30分在南海海域A处巡逻,观测到岛礁B在北偏东60°,该船以每小时10海里的速度向正东航行到C处,观测岛礁B在北偏东30°,继续向正东航行到D处时,再观测到岛礁B在北偏西30°,当海监船到达C处时恰与岛礁B相距20海里,请你分别确定“中国海监50”从A处到达C处和D处所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数的自变量x满足 ![]() ≤x≤2时,函数值y满足
≤x≤2时,函数值y满足 ![]() ≤y≤1,则下列函数①y=
≤y≤1,则下列函数①y= ![]() x,②y=
x,②y= ![]() ,③y=
,③y= ![]() ,④y=﹣
,④y=﹣ ![]() x+
x+ ![]() ,⑤y=(x﹣1)2 , 符合条件的函数有( )
,⑤y=(x﹣1)2 , 符合条件的函数有( )
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AF∥DE,B为AF上一点,∠ABC=60°,交ED于C,CM平分∠BCE,∠MCN=90°.
(1)求∠DCN的度数;
(2)若∠CBF的平分线交CN于N,求证:BN∥CM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尝试探究并解答:
(1)为了求代数式x2+2x+3的值,我们必须知道x的值,若x=1,则这个代数式的值为 ;若x=2,则这个代数式的值为 ,可见,这个代数式的值因x的取值不同而 (填“变化”或“不变”).尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)本学期我们学习了形如a2+2ab+b2及a2﹣2ab+b2的式子,我们把这样的多项式叫做“完全平方式”在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式同样地,把一个多项式进行部分因式分解可以解决代数式的最大(或最小)值问题例如:x2+2x+3=(x2+2x+1)+2=(x+1)2+2,因为(x+1)2≥0,所以(x+1)2+2≥2,所以这个代数式x2+2x+3有最小值是2,这时相应的x的值是 .
(3)猜想:①4x2﹣12x+13的最小值是 ;
②﹣x2﹣2x+3有 值(填“最大”或“最小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分:
类别 | A | B | C | D | E |
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 12 | 30 |
| 54 | 9 |

根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有多少人,这些学生数占被调查总人数的百分比为多少;
(2)被调查学生的总人数为多少人,统计表中![]() 的值为多少,统计图中
的值为多少,统计图中![]() 的值为多少;
的值为多少;
(3)求在统计图中,B类所对应扇形圆心角的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com