
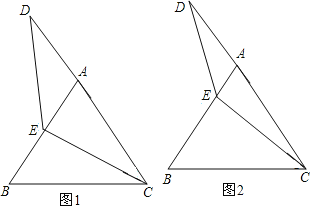
【题目】等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题:
(1)如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:AD BE;
(2)如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。
【答案】(1)AD=BE;(2)证明见解析
【解析】分析:(1)根据题意易得∠D=∠AED=30°,即可得AD=AE,再根据AE=BE,即可解题;
(2)通过作EF∥AC构造等边三角形把BE转化为EF,再利用“角角边”易证△AED≌△FCE,可得AD=FE,即可解题.
本题解析:
(1)AD=BE;
(2)过点E作EF∥AC交BC于点F,
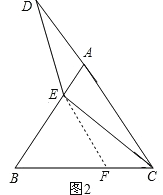
∴∠EFB=∠ACB,∠BEF=∠BAC,∠FEC=∠ECA,
∵△ABC是等边三角形,
∴∠ACB=∠BAC=∠B=60°,
∴∠EFB=∠BEF=∠B=60°,
∴△BEF是等边三角形,
∴BE=EF,
∵ED=EC,
∴∠D=∠ECA,
∴∠D=∠FEC,
∵∠BFE=∠BAC=60°,
∴∠EAD=∠CFE=120°,
在△AED和△FCE中,
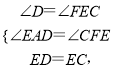
∴△AED≌△FCE(AAS),
∴AD=FE,
∴AD=BE。


科目:初中数学 来源: 题型:
【题目】寿县教育部门计划在3月12日植树节当天安排![]() ,
,![]() 两校部分学生到森林公园参加植树活动.已知
两校部分学生到森林公园参加植树活动.已知![]() 校区的每位学生往返车费是6元,
校区的每位学生往返车费是6元,![]() 校每位学生的往返车费是10元,要求两所学校均要有学生参加,且
校每位学生的往返车费是10元,要求两所学校均要有学生参加,且![]() 校参加活动的学生比
校参加活动的学生比![]() 校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求
校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求![]() ,
,![]() 两校最多各有多少学生参加?
两校最多各有多少学生参加?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( ) 
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
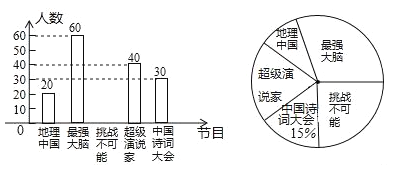
【题目】我市某中学为了了解孩子们对《中国诗词大会》、《挑战不可能》、《最强大脑》、《超级演说家》、《地理中国》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:
(1)本次调查中共抽取了 名学生.
(2)补全条形统计图.
(3)在扇形统计图中,喜爱《地理中国》节目的人数所在的扇形的圆心角是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1 . 试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原来正方形面积的 ![]() ,请说明理由.(写出证明及计算过程)
,请说明理由.(写出证明及计算过程) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
.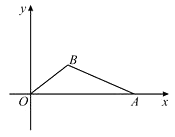
(1)①在图中,求作△ABO的外接圆;(尺规作图,不写作法但需保留作图痕迹);②求点B的坐标与cos∠BAO的值;
(2)若A,O位置不变,将点B沿 ![]() 轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.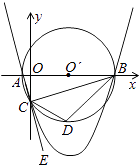
(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 16 | 18 | 30 | 35 |
水费(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是______.
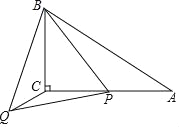
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com