
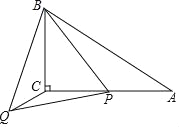
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是______.
科目:初中数学 来源: 题型:
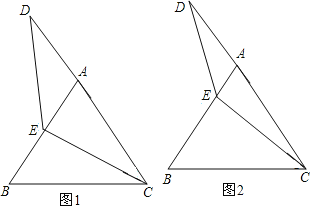
【题目】等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题:
(1)如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:AD BE;
(2)如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠C=90°,沿过点A的一条直线AE折叠Rt△ABC,使点C恰好落在AB边的中点D处,则∠B的度数是( )

A. 25° B. 30° C. 40° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全下列解题过程:
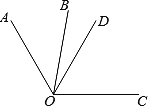
如图,OD是∠AOC的平分线,且∠BOC-∠AOB=40°,若∠AOC=120°,求∠BOD的度数.
解:∵OD是∠AOC的平分线,∠AOC=120°
∴∠DOC=![]() ∠_______=______°.
∠_______=______°.
∵∠BOC+∠_____=120°,∠BOC-∠AOB=40°
∴∠BOC=80°
∴∠BOD=∠BOC-∠______=______°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个等腰直角△ABC和△CDE,它们的两个直角顶点B、D在直线MN上,过点A、E分别作AG⊥MN,EF⊥MN,垂足分别为G、F.
(1)如图1,当△ABC和△CDE在△BCD的外部时,请你探索线段EF、DB、AG之间的数量关系,其数量关系为______.
(2)如图2,将图1中的△ABC沿BC翻折,其他条件不变,那么(1)中的结论是否仍然成立?若成立,请你给出证明,若不成立,请探索它们的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
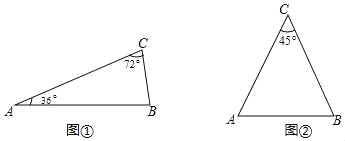
(理解)如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
(应用)
(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值______;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边的中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边的中点,得到四边形A2B2C2D2;…;如此进行下去,得到四边形A7B7C7D7,那么四边A7B7C7D7形的周长为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com