
【题目】(定义)数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
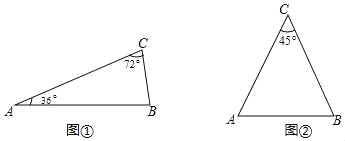
(理解)如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
(应用)
(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值______;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
【答案】【定义】见解析;【应用】(1)84°或103.5°或124°或117°或126°;(2)画图见解析;∠B=42°或18°.
【解析】
【定义】
如图①,如图②所示,根据题意画出图形即可;
【应用】(1)①如图③当∠B=42°,AD为“好线”,②如图④当∠B=42°,AD为“好线”,③如图⑤当∠ABC=42°时,BD为“好线”,④如图⑥,当∠B=42°时,CD为“好线”,⑤如图⑦,当∠B=42°时,CD为“好线”,根据等腰三角形的性质即可得到结论;
(2)设∠B=x°,①当AD=DE时,如图1(a),②当AD=AE时,如图1(b),③当EA=DE时,根据等腰三角形的性质列方程即可得到结论.
解:(定义)如图①,如图②所示,
(应用)
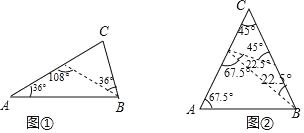
(1)①如图③当∠B=42°,AD为“好线”,
则AD=AD=BD,故这个三角形最大内角是∠C=84°;
②如图④当∠B=42°,AD为“好线”,
则AB=AD,AD=CD,这个三角形最大内角是∠BAC=103.5°;
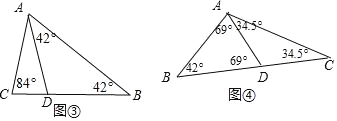
③如图⑤当∠ABC=42°时,BD为“好线”,
则AD=BD,CD=BC,故这个三角形最大内角是∠C=124°,
④如图⑥,当∠B=42°时,CD为“好线”,
则AD=CD=BC,故这个三角形最大内角是∠ACB=117°,
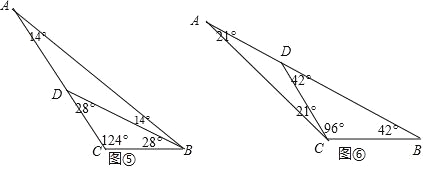
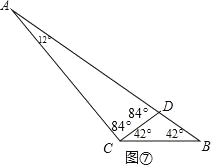
⑤如图⑦,当∠B=42°时,CD为“好线”,
则AD=AC,CD=BD,故这个三角形最大内角是∠ACB=126°,
综上所述,这个三角形最大内角的所有可能值是84°或103.5°或124°或117°或126°,
故答案为:84°或103.5°或124°或117°或126°;
(2)设∠B=x°,
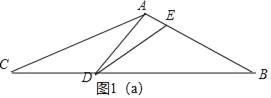
①当AD=DE时,如图1(a),
∵AD=CD,
∴∠C=∠CAD=27°,
∵DE=EB,
∴∠B=∠EDB=x°
∴∠AED=∠DAE=2x°,
∴27×2+2x+x=180,
∴x=42,
∴∠B=42°;
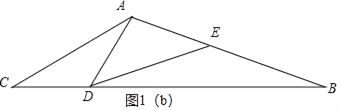
②当AD=AE时,如图1(b),
∵AD=CD,
∴∠C=∠CAD=27°,
∵DE=EB,
∴∠B=∠EDB=x°
∴∠AED=∠ADE=2x°,
∴2x+x=27+27,
∴x=18,
∴∠B=18°.
③当EA=DE时,
∵90﹣x+27+27+x=180,
∴x不存在,应舍去.
综合上述:满足条件的x=42°或18°.


科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 16 | 18 | 30 | 35 |
水费(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是______.
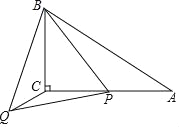
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同.
(1)摸出1个球是白球的概率是;
(2)同时摸两个球恰好是两个红球的概率(要求画树状图或列表).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具零售店准备从批发市场选购A、B两种文具,批发价A种为12元/件,B种为8元/件.若该店零售A、B两种文具的日销售量y(件)与零售价x(元/件)均成一次函数关系.(如图) 
(1)求y与x的函数关系式;
(2)该店计划这次选购A、B两种文具的数量共100件,所花资金不超过1000元,并希望全部售完获利不低于296元,若按A种文具每件可获利4元和B种文具每件可获利2元计算,则该店这次有哪几种进货方案?
(3)若A种文具的零售价比B种文具的零售价高2元/件,求两种文具每天的销售利润W(元)与A种文具零售价x(元/件)之间的函数关系式,并说明A、B两种文具零售价分别为多少时,每天销售的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角坐标平面内两点A(-2,-3)、B(3,-3),将点B向上平移5个单位到达点C,求:

(1)A、B两点间的距离;
(2)写出点C的坐标;
(3)四边形OABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com