
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
【答案】D
【解析】
先根据邻补角的定义可求得∠EFD=70°,再根据角平分线的定义求得∠EFM=35°,由平移的性质可得GN//FM,继而可得∠EGN=∠EFM=35°,再根据AB//CD,可得∠AGE=∠EFC=110°,再由∠AGN=∠AGE+∠EGN即可得解.
∵∠EFC=110°,∠EFC+∠EFD=180°,
∴∠EFD=70°,
∵FM平分∠EFD,
∴∠EFM=35°,
∵将射线FM平移,使得端点F与点G重合且得到射线GN,
∴GN//FM,
∴∠EGN=∠EFM=35°,
∵AB//CD,
∴∠AGE=∠EFC=110°,
∴∠AGN=∠AGE+∠EGN=110°+35°=145°,
故选D.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代对勾股定理有深刻的认识.
(1)三国时代吴国数学家赵爽第一次对勾股定理加以证明:用四个全等的图1所示的直角三角形拼成一个图2所示的大正方形,中间空白部分是一个小正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a,b,求(a+b)2的值;
(2)清朝的康熙皇帝对勾股定理也很有研究,他著有《积求勾股法》:用现代的数学语言描述就是:若直角三角形的三边长分别为3,4,5的整数倍,设其面积为S,则求其边长的方法为:第一步![]() =m;第二步:
=m;第二步: ![]() =k;第三步:分别用3,4,5乘k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.
=k;第三步:分别用3,4,5乘k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某绿色无公害蔬菜基地有甲、乙两种植户,他们们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积(单位:亩) | 种植B类蔬菜面积(单位:亩) | 总收入(单位:元) |
甲 | 1 | 3 | 13500 |
乙 | 2 | 2 | 13000 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)今年甲、乙两种植户联合种植,计划合租50亩地用来种植A、B两类蔬菜,为了使总收入不低于16400元,问联合种植最多可以种植A类蔬菜多少亩?
查看答案和解析>>
科目:初中数学 来源: 题型:
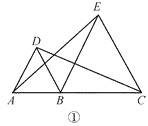
【题目】在直线上顺次取 A,B,C 三点,分别以 AB,BC 为边长在直线的同侧作正三角形, 作得两个正三角形的另一顶点分别为 D,E.
(1)如图①,连结 CD,AE,求证:CD=AE;
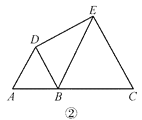
(2)如图②,若 AB=1,BC=2,求 DE 的长;
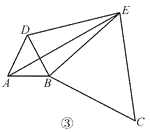
(3)如图③,将图②中的正三角形 BCE 绕 B 点作适当的旋转,连结 AE,若有 DE2+BE2= AE2,试求∠DEB 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有红、黄、蓝三种颜色的球(除颜色以外,其余都相同),其中红球2个,黄球2个,从中随机摸出一个球是蓝色球的概率为![]() .
.
(1)求袋子里蓝色球的个数;
(2)甲、乙两人分别从袋中摸出一个球(不放回),求摸出的两个球中一个是红球一个是黄球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列哪组条件能够判别四边形ABCD是平行四边形?( )
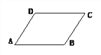
A. AB∥CD,AD=BC B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D D. AB=AD,CB=CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com