
【题目】我市某绿色无公害蔬菜基地有甲、乙两种植户,他们们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积(单位:亩) | 种植B类蔬菜面积(单位:亩) | 总收入(单位:元) |
甲 | 1 | 3 | 13500 |
乙 | 2 | 2 | 13000 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)今年甲、乙两种植户联合种植,计划合租50亩地用来种植A、B两类蔬菜,为了使总收入不低于16400元,问联合种植最多可以种植A类蔬菜多少亩?
【答案】(1)A、B两类蔬菜每亩平均收入各是3000元、3500元;(2)联合种植最多可以种植A类蔬菜22亩.
【解析】
(1)设A、B两类蔬菜每亩平均收入各是x元、y元,根据等量关系甲种植户总收入13500元,乙种植户总收入13000元列方程组进行求解即可得;
(2)设种植A类蔬菜a亩,则种植B类蔬菜(50-a)亩,根据总收入不低于16400元列不等式进行求解即可得.
(1)设A、B两类蔬菜每亩平均收入各是x元、y元,
根据题意得:![]() ,
,
解得:![]() ,
,
答:A、B两类蔬菜每亩平均收入各是3000元、3500元;
(2)设种植A类蔬菜a亩,则种植B类蔬菜(50-a)亩,
根据题意得:3000a+3500(50-a)≥164000,
解得:a≤22,
答:联合种植最多可以种植A类蔬菜22亩.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】有一列数,第一个数为x1=1,第二个数为x2=3,从第三个数开始依次为x3,x4,…,xn,….从第二个数开始,每个数是左右相邻两个数和的一半,如x2=![]() ,x3=
,x3=![]() .
.
(1)求x3,x4,x5的值,并写出计算过程;
(2)根据(1)的结果,推测x9等于多少;
(3)探索这一列数的规律,猜想第k(k为正整数)个数xk等于多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产,若购买3盒豆腐乳和2盒猕猴桃果汁共需60元;购买1盒豆腐乳和3盒猕猴桃果汁共需55元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,端点为P的两条射线分别交两直线l1、l2于A、C、B、D四点,已知∠PBA=∠PDC,∠l=∠PCD,求证:∠2+∠3=180°.
证明:∵∠PBA=∠PDC( )
∴ (同位角相等,两直线平行)
∴∠PAB=∠PCD( )
∵∠1=∠PCD( )
∴ (等量代换)
∴PC//BF(内错角相等,两直线平行),
∴∠AFB=∠2( )
∵∠AFB+∠3=180°( )
∴∠2+∠3=180°(等量代换)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了计算河的宽度,某学习小组在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使E C⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=160 米,DC=80米,E C=49米,求A、B间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12).
(1)当x=9时,求BM的长和△ABM的面积;
(2)是否存在点M,使MDDC=20?若存在,请求出x的值;若不存在,请说明理由.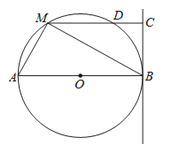
查看答案和解析>>
科目:初中数学 来源: 题型:
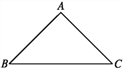
【题目】如果经过三角形某一个顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.
(1)如图,已知等腰直角三角形ABC,∠A=90°,试说明:△ABC是生成三角形;
(2)若等腰三角形DEF有一个内角等于36°,请你画出简图说明△DEF是生成三角形.(要求画出直线,标注出图中等腰三角形的顶角、底角的度数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com